Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ДЛИНА ОКРУЖНОСТИ - ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА
|
Цель деятельности учителя |
Создать условия для выведения формул, для выражения длины окружности через ее радиус, для вычисления длины / дуги окружности с градусной мерой α |
|||
|
Термины и понятия |
Окружность, длина дуги окружности |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют объяснять понятие длины окружности, выводить формулу для нахождения длины окружности |
Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации; осознанно владеют логическими действиями. Регулятивные: умеют контролировать процесс и результат учебной математической деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют познавательный интерес к изучению предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для математического диктанта; • загадки геометрического содержания; • исторические сведения об окружности |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Выявить трудности, возникшие при выполнении домашнего задания |
(Ф/И) 1. Проверить выполнение домашней работы. 2. Разобрать задачи, вызвавшие наибольшие затруднения. 3. Провести математический диктант (15 мин). (Учащиеся выполняют задания на листочках и сдают на проверку учителю.) Вариант I 1. Найдите угол правильного десятиугольника. 2. Найдите сторону правильного треугольника, если радиус описанной около него окружности равен 2 м. 3. Найдите радиус окружности, вписанной в правильный треугольник, если радиус описанной около него окружности равен 2 м. 4. Найдите площадь правильного треугольника, если расстояние от его центра до вершины равно 2 м. 5. Закончите предложение: “Угол с вершиной в центре окружности называется...” 6. Угол с вершиной в центре правильного многоугольника и сторонами, проходящими через две его соседние вершины, равен 36°. Сколько сторон имеет этот многоугольник? 7. Чему равен cos0°? 8. С помощью циркуля и линейки постройте правильный шестиугольник. Вариант II 1. Сколько сторон имеет правильный многоугольник, если его сторона стягивает дугу описанной окружности, равную 18°? 2. Найдите площадь квадрата, если радиус описанной около него окружности равен 2 дм. 3. Закончите предложение: “Кругом называется часть плоскости...” 4. Найдите сторону квадрата, если расстояние от его центра до вершины равно 2 дм. 5. Найдите радиус окружности, вписанной в квадрат, если радиус описанной около него окружности равен 2 дм. 6. Чему равен cos0°? 7. Найдите угол правильного девятиугольника. 8. С помощью циркуля и линейки постройте правильный треугольник |
|||
|
II этап. Изучение нового материала |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Вывести формулу для вычисления длины окружности |
(Ф/И) 1. Отгадывание загадок. Нет углов у меня, И похож на блюдце я, На тарелку и на крышку, На кольцо, на колесо. Кто же я такой, друзья? (Круг.) У круга есть одна подруга, Знакома всем её наружность. Она идет по краю круга И называется... (окружность). 2. Изложение материала. Объяснение можно организовать в виде беседы. При этом можно обсудить следующие вопросы: - Как можно измерить длину обруча? - На доске начерчена окружность. Как измерить длину этой окружности? (Формулу, которую изучали в курсе математики 6 класса, использовать нельзя.) Варианты ответов: а) с помощью нити; б) вписать многоугольник с достаточно большим числом сторон и найти его периметр. 3. Вывод формулы длины окружности (можно провести в виде лекции). Пусть имеются две окружности с радиусами R1 и R2, а их длины равны С1 и С2 соответственно. Впишем в каждую из них n-угольники и найдем отношение их периметров Р1 и Р2. Р1 = n ∙ а1, Р2 = n ∙ а2, где а1 и а2 - стороны наших n-угольников. Используя формулу По свойству пропорций: так как Ранее было установлено, что при n → ∞ Р1→ С1, Р2→ С2, поэтому Итак, Формула для вычисления длины окружности: С = 2πR. Число π является приближенным (π ≈ 22/7), его значение было найдено еще в III веке до нашей эры греческим ученым Архимедом. При решении задач чаще используют приближенное значение я, равное 3,14. 4. Историческая справка. Многие геометрические фигуры, в том числе и окружность, были известны с давних времен. В разные времена в разных странах значения я были различны. Так, например, в Древнем Египте 3500 лет назад π равнялось 3,16; у древних римлян - 3,12. Согласно подсчетам Архимеда, π = 22/7. Для запоминания этого числа может быть полезно стихотворение: Двадцать две совы скучали На больших сухих суках, Двадцать две совы мечтали О семи больших мышах: О мышах довольно юрких В аккуратных серых шкурках. Слюнки капали с усов У огромных серых сов. Вот еще несколько фактов из истории числа π. Обозначение числа происходит от греческого perijerio “переферия”, что в переводе означает “окружность”. Впервые обозначение использовал английский математик Уильямс Джонс в 1706 году. В России со времен Петра I занимались геометрическими расчетами в астрономии, машиностроении, корабельном деле. Значение числа π - 3,1415926. Для его запоминания придумано двустишие в учебнике Магницкого, написанное по правилам старой русской орфографии: “Кто и шутя и скоро пожелать пи узнать число ужъ знаетъ”. У числа π есть день рождения, он отмечается 14 марта (этот день записывается в американском формате дат (месяц/день) как 3,14) и начинается в 1.59. Еще одной датой, связанной с числом я, является 22 июля, так как в европейском формате дат этот день записывается как 22/7. В этот день в Италии едят ПИццу, в Германии свиной - шПИк, в Англии жареную - ПИкшу, во Франции - что-нибудь ПИкантное, в России стряпают ПИроги. 5. Вывод формулы длины дуги окружности (можно провести в виде ответов на вопросы). - Какую часть окружности составляет дуга в 1°? - Чему равна длина дуги в 1 °? - Чему равна длина дуги в α. Вывод: длина дуги с градусной мерой α равна |
|||
|
III этап. Закрепление изученного материала |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Закрепить полученные знания |
(Ф/И) 1. Решить задачу № 1101 (таблицу начертить заранее на доске). 2. Решить задачи № 1102 и 1103 (устно). 3. Решить задачу № 1109 (а, б). 4. Решить задачу № 1111 (использовать рис. 316 на с. 282) |
|||
|
IV этап. Итоги урока |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - Какую формулу вспомнили и доказали на уроке? - Чему равно число Архимеда? |
(И) Домашнее задание: изучить материал пункта 114; решить задачи № 1109 (в, г), 1106, 1104 (а), 1105 (а) |
|||
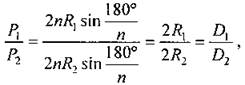 где D1 и D2 - диаметры окружностей.
где D1 и D2 - диаметры окружностей.