ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 8 КЛАССА - Урок 2

Цель деятельности учителя

Создать условия для обобщения и систематизации сведений, необходимых при изучении геометрии в 9 классе, повторения некоторых свойств треугольников и четырехугольников, закрепления знаний учащихся в ходе решения задач

Термины и понятия

Параллелограмм, прямоугольник, трапеция, ромб, треугольник, высота; окружность, вписанная в треугольник; центральный угол, вписанный угол, хорда

Планируемые результаты

Предметные умения

Универсальные учебные действия

Имеют систематические знания о плоских фигурах и их свойствах

Познавательные: понимают и используют математические средства наглядности, для иллюстрации, интерпретации, аргументации.

Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей.

Коммуникативные: выстраивают аргументацию, участвуют в диалоге, приводят примеры и контрпримеры.

Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И)

Образовательные

ресурсы

• Чертежи к задачам

I этап. Решение задач

Цель деятельности

Совместная деятельность

Обобщить и систематизировать знания по изученному материалу 8 класса

(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию.

(П) 2. Решение задач.

1) Найдите длины отрезков, соединяющих середины сторон трапеции с равными диагоналями, если ее основания равны 7 см и 9 см, а высота равна 8 см.

2) Вычислите площадь треугольника АВС, если А В = 8,5 м, АС = 5 м, высота AN = 4 м и точка N лежит на отрезке ВС.

3) Вершины четырехугольника ABCD являются серединами сторон четырехугольника, диагонали которого равны 6 дм и пересекаются под углом 60°. Вычислите площадь четырехугольника ABCD.

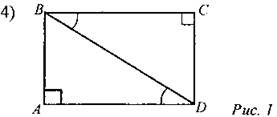
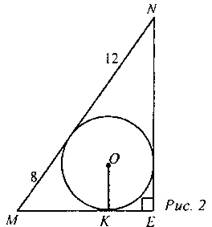
Дано: ∠BAD = ∠BCD = 90°, ∠CBD = ∠ADB.

Доказать: АВ = CD.

(Ф) 3. Решение задач по готовым чертежам.

1) Дано: ∆MEN - прямоугольный.

Найти: OK.

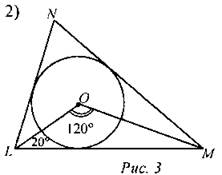
Дано: ∆LMN и вписанная в него окружность.

Найти: ∠N.

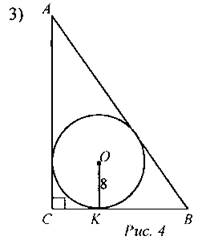
Дано: ∆ABC - прямоугольный, АВ = 52.

Найти: Р_ABC.

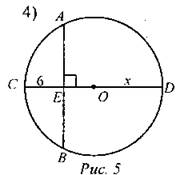
Дано: АВ + СЕ = CD.

Найти: OD.

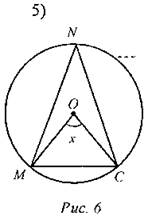
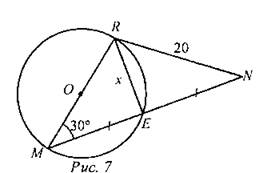
Дано: ∠NMC = 75°, ∪NM: ∪МС = 2 : 1.

Найти: ∠O.

6) Найти: RE.

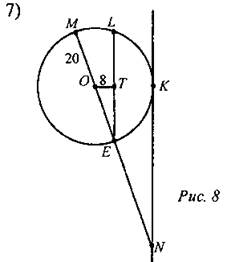
Дано: EL ll NK.

Найти: MN.

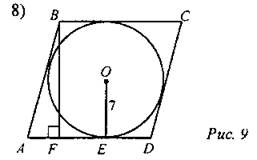
Дано: ABCD - ромб.

Найти: BF.

II этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Какие темы повторили на уроке?

- Задайте три вопроса по теме урока

(И) Домашнее задание: решить задачи № 515, 517, 524