Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 8 КЛАССА
|
Цель деятельности учителя |
Создать условия для обобщения и систематизации сведений, необходимых при изучении геометрии в 9 классе, повторения некоторых свойств треугольников и четырехугольников, закрепления знаний учащихся в ходе решения задач |
||
|
Термины и понятия |
Параллелограмм, прямоугольник, трапеция, ромб, треугольник, площади, теорема Пифагора |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Владеют систематическими знаниями о плоских фигурах и их свойствах |
Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: выстраивают аргументацию, участвуют в диалоге, приводят примеры и контрпримеры. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И); групповая (Г) |
||
|
Образовательные ресурсы |
• Геометрия. 7-9 классы: учеб, для общеобразоват. учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. М.: Просвещение, 2014*. • Готовые чертежи к заданиям |
||
|
I этап. Актуализация опорных знаний |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Повторить изученный в 8 классе материал |
(Ф) Теоретический опрос: - Дайте определение параллелограмма. Перечислите его свойства и признаки. - Дайте определение прямоугольника. Перечислите его свойства и признаки. - Дайте определение ромба. Перечислите его свойства и признаки. - Дайте определение трапеции. Назовите виды трапеций. Перечислите свойства равнобедренной трапеции |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Систематизировать теоретические знания при решении задач на повторение |
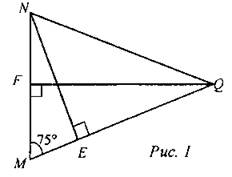
(Г) 1. Решение задач: 1) Докажите, что центр окружности, вписанной в равнобедренный треугольник, лежит на высоте, проведенной к основанию. 2) Докажите, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к его основанию, или на ее продолжении. 3) Докажите, что треугольник является равнобедренным, если две его медианы равны. 4) Докажите, что если в треугольнике две высоты равны, то центр вписанной в него окружности лежит на одной из медиан этого треугольника, а центр описанной окружности - на той же медиане или ее продолжении. 5) Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма. (П) 2. Решение задач по готовым чертежам. 1) Дано: NQ = MQ. Найти: NE/QF.
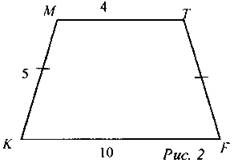
2) Дано: KMTF - трапеция. Найти: sin∠K, cos∠K.
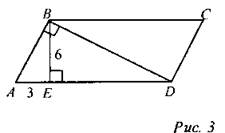
3) Дано: ABCD - параллелограмм. Найти: SABCD.
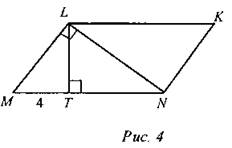
4) Дано: MLKN - параллелограмм. MN : ML = 2 : 1. Найти: SMLKN.
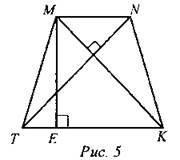
5) Дано: TMNK - трапеция. МК = 15, ME = 9. Найти: STMNK.
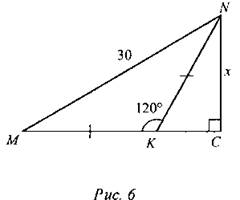
6) Найти: NC.
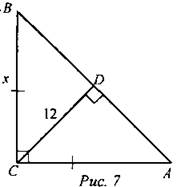
7) Найти: ВС.
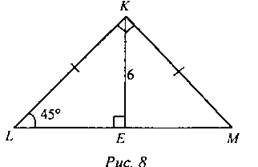
8) Найти: LM.
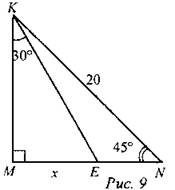
9) Найти: MN.
|
||
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Какие темы повторили на уроке? - Что еще, по вашему мнению, предстоит повторить на следующем уроке? |
(И) Домашнее задание: повторить материал пунктов 15; 17-20; 30; 42-46; 49-55; решить задачи № 167, 163, 502, 513 |
||
* Здесь и далее по всему пособию на каждом уроке предполагается работа с учебником. В связи с этим далее ссылка на учебник будет опущена.