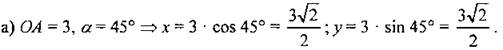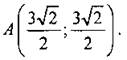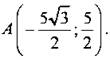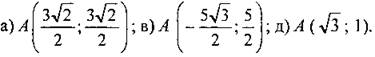Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
СИНУС, КОСИНУС, ТАНГЕНС УГЛА - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
|
Цели деятельности учителя |
Совершенствовать навыки нахождения синуса, косинуса, тангенса для углов от 0° до 180°; способствовать развитию умения пользоваться основным тригонометрическим тождеством |
||
|
Термины и понятия |
Единичная окружность, синус, косинус, тангенс, котангенс, основное тригонометрическое тождество |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют применять определения синуса, косинуса, тангенса и котангенса для определения координаты точки единичной окружности |
Познавательные: осознанно владеют логическими действиями определения понятий. Регулятивные: умеют осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в группе, ясно, точно, грамотно излагать свои мысли. Личностные: осознают важность и необходимость знаний в жизни человека |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||
|
Образовательные ресурсы |
• Задания для математического диктанта |
||
|
I этап. Актуализация знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Повторить определения синуса, косинуса, тангенса |
(Ф/И) 1. Проверка выполнения домашнего задания. (Двое учащихся у доски.) 2. Математический диктант (10-12 мин). Вариант I 1. Стороны прямоугольного треугольника равны 3 см, 4 см и 5 см. Найдите синус, косинус и тангенс меньшего острого угла этого треугольника. 2. Катет прямоугольного треугольника равен 6 дм, а противолежащий угол равен 30°. Найдите гипотенузу этого треугольника. 3. Вычисляя синус острого угла, ученик получил число 1,05. Верны ли его вычисления? 4. Найдите косинус острого угла, если его синус равен 12/13. 5. Найдите тангенс острого угла, если его синус равен 12/13. 6. Синус острого угла прямоугольного треугольника равен 9/41. Чему равен косинус второго острого угла этого треугольника? Вариант II 1. Стороны прямоугольного треугольника равны 10 дм, 8 дм и 6 дм. Найдите синус, косинус и тангенс большего острого угла этого треугольника. 2. Катет прямоугольного треугольника равен 8 см, а противолежащий угол равен 45°. Найти гипотенузу этого треугольника. 3. Вычисляя косинус острого угла прямоугольного треугольника, ученик получил число 1,05. Верны ли его вычисления? 4. Найдите синус острого угла, если его косинус равен 24/25. 5. Найдите тангенс острого угла, если его косинус равен 24/25. 6. Косинус острого угла прямоугольного треугольника равен 12/37. Чему равен синус второго острого угла этого треугольника? |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать навыки решения задач |
(Г) 1. Решить задачи № 1017 (б), 1018 (а) в малых группах. Варианты решений обсудить. 2. Самостоятельно решить № 1018 (а, в, д), 1019 (б, г) |
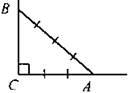
№ 1017 (б).
Так как косинус угла - это отношение прилежащего катета к гипотенузе и cos∠A = 3/4, то для построения угла А надо построить прямоугольный ∆ACB, в котором АС = 3, АВ = 4. № 1018. Если точка А имеет координаты (х; у), то х = ОА ∙ cosα, а у = ОА ∙ sinα.
To есть
To есть
Ответ: № 1019. Координаты точки А можно вычислить по формулам: х = ОА ∙ cosα, у = ОА ∙ sinα. В прямоугольной системе координат ХОУ для координат точки А выполняется равенство х2 + у2 = ОА2. б) А(0; 3), тогда
Ответ: б) 90°; г) 135° |
|
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Подведите итог урока. Достигли ли мы поставленных целей? - Оцените свою работу. Что для вас оказалось наиболее сложным? |
(И) Домашнее задание: решить № 1017 (а, в), 1018 (б, г), 1019 (а, в) |
||