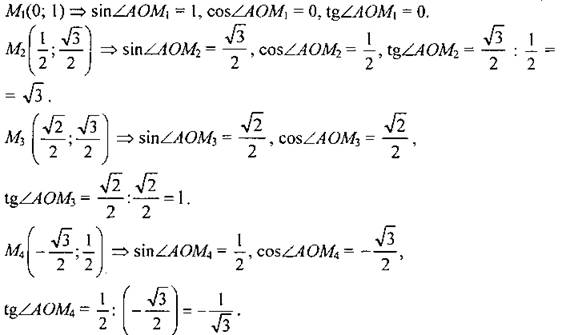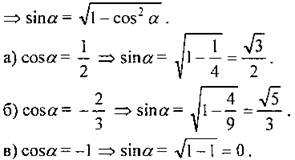Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
СИНУС, КОСИНУС, ТАНГЕНС, КОТАНГЕНС - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
|
Цель деятельности учителя |
Создать условия для введения понятий синуса, косинуса, тангенса и котангенса для углов от 0° до 180°, выведения основного тригонометрического тождества |
|||||||||||||||||||
|
Термины и понятия |
Единичная окружность, синус, косинус, тангенс, котангенс, основное тригонометрическое тождество |
|||||||||||||||||||
|
Планируемые результаты |
||||||||||||||||||||
|
Предметные умения |
Универсальные учебные действия |
|||||||||||||||||||
|
Умеют применять определения синуса, косинуса, тангенса и котангенса для определения координаты точки единичной окружности |
Познавательные: осознанно владеют логическими действиями определения понятий. Регулятивные: умеют осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, ясно, точно, грамотно излагать свои мысли. Личностные: понимают важность и необходимость изучения предмета в жизни человека |
|||||||||||||||||||
|
Организация пространства |
||||||||||||||||||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||||||||||||||||||
|
Образовательные ресурсы |
• Тест |
|||||||||||||||||||
|
I этап. Актуализация знаний учащихся |
||||||||||||||||||||
|
Цель деятельности |
Совместная деятельность |
|||||||||||||||||||
|
Пояснить ошибки, допущенные в контрольной работе |
(Ф/И) 1. Сообщить результат контрольной работы. 2. Прокомментировать основные ошибки |
|||||||||||||||||||
|
II этап. Мотивация к деятельности |
||||||||||||||||||||
|
Цель деятельности |
Совместная деятельность |
|||||||||||||||||||
|
Через повторение изученного материала подвести учащихся к восприятию новой темы |
(Ф/И) 1. Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника? 2. Какое равенство называют основным тригонометрическим тождеством? 3. Чему равны значения синуса, косинуса и тангенса для углов 30°, 45° и 60°? (И) Тест с последующей самопроверкой.
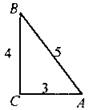
1. Дан треугольник АВС. Чему равен синус угла А?
2. Чему равен тангенс угла В?
3. Чему равен косинус 60°?
4. Если sinα = 5/9, то чему равен cosα?
5. Если cosα = 1/3, то чему равен tgα?
6. В прямоугольном ∆АСВ, sinA = 2/5. Найти sinB.
7. Упростите выражение: sin30° ∙ cos45° ∙ tg60°.
|
|||||||||||||||||||
|
Ответы: |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||||||||||
|
а |
в |
б |
в |
а |
б |
а |
||||||||||||||
|
III этап. Изучение новой темы |
||||||||||||||||||||
|
Цель деятельности |
Совместная деятельность |
|||||||||||||||||||
|
Ввести понятия синуса, косинуса, тангенса и котангенса через координаты точки единичной окружности |
(Ф) 1. Ввести понятие единичной полуокружности (с. 248, рис. 290). 2. Ввести понятие синуса и косинуса для углов 0° ≤ α ≤ 180°: sinα = у; cosα = х. Таким образом, для любого угла а из промежутка 0° ≤ α ≤ 180° синусом угла а называется ордината у точки М, а косинусом угла α - абсцисса х точки М, лежащей на единичной полуокружности. 0 ≤ sinα ≤ 1; -1 ≤ cosα ≤ 1. 3. Найти значения синуса и косинуса для углов 0°, 90° и 180°. 4. Определить тангенс угла α (α ≠ 90°): 5. Вывести основное тригонометрическое тождество sin2α + cos2α = 1, используя рис. 290 в учебнике на с. 248. 6. Составить таблицу: |
|||||||||||||||||||
|
0° |
30° |
45° |
60° |
90° |
120° |
135° |
150° |
180° |
||||||||||||
|
sinα |
||||||||||||||||||||
|
cosα |
||||||||||||||||||||
|
tgα |
||||||||||||||||||||
|
Значения для углов от 0° до 90° учащиеся заполняют самостоятельно (материал 8 класса). Остальные значения заполняют с помощью учителя, используя формулы приведения и единичную окружность |
||||||||||||||||||||
|
IV этап. Закрепление изученного материала |
||||||||||||||||||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||||||||||||||||||
|
В процессе решения простых задач отработать понятия синуса, косинуса, тангенса и котангенса |
(Ф/И) 1. Решить № 1011 (устно). 2. Решить № 1012 на доске и в тетрадях. 3. Решить № 1013 на доске и в тетрадях |
№ 1012. Решение: Точка с координатами (х; у) принадлежит единичной полуокружности, если выполняются условия: -1 ≤ х ≤ 1, -1 ≤ у ≤ 1 и х2 + у2 = 1. Точка М1 (0; 1) удовлетворяет всем условиям => она лежит на единичной полуокружности. Точка Точки Синус ∠AOM - это ордината точки М. Косинус ∠AOM - это абсцисса точки М. Тангенс ∠AOM равен отношению синуса ∠AOM к его косинусу.
№ 1013. Решение:
Ответ: |
||||||||||||||||||
|
V этап. Итоги урока. Рефлексия |
||||||||||||||||||||
|
Деятельность учителя |
Деятельность учащихся |
|||||||||||||||||||
|
(Ф/И) - Что повторили на уроке? - Что является абсциссой точки единичной окружности? Ординатой точки единичной окружности? |
(И) Домашнее задание: изучить материал пунктов 97-99; ответить на вопросы 1-4, с. 266; решить задачи № 1014, 1015 |
|||||||||||||||||||
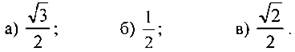
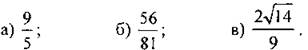
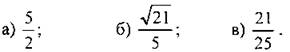
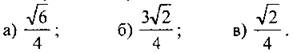
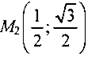 удовлетворяет всем условиям => она лежит на единичной полуокружности.
удовлетворяет всем условиям => она лежит на единичной полуокружности.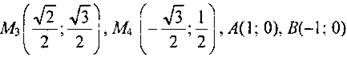 также лежат на единичной полуокружности.
также лежат на единичной полуокружности.