Контрольные и самостоятельные работы по алгебре и геометрии 9 класс - 2016 год
Подобие фигур - КОНТРОЛЬНЫЕ РАБОТЫ - ГЕОМЕТРИЯ
(по учебнику А.В. Погорелова)
K1. Подобие фигур
Вариант 1
1. Стороны треугольника равны 3 см, 4 см и 5 см. Найдите стороны подобного ему треугольника, периметр которого равен 48 см.
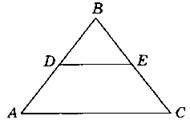
2. Дано: АВ = 6 см; АС = 9 см; ВС = 12 см; BE = 4 см; BD = 2 см. Доказать: ΔАВС ~ ΔBDE. Найти: DE.
3. Найдите две стороны треугольника, если их сумма равна 14 см, а биссектриса угла между ними делит третью сторону в отношении 3:4.
Вариант 2
1. Стороны треугольника относятся как 2:7:6. Найдите стороны подобного ему треугольника, периметр которого равен 75 см.
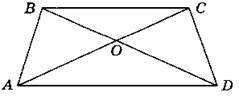
2. Дано: АО = 20 см; ВО = 3 см; АС = 26 см; DO = 10 см; ВС = 9 см. Доказать: ΔAOD ~ ΔВОС. Найти: AD.
3. Найдите две стороны треугольника, если их разность равна 2 см, а биссектриса угла между ними делит третью сторону на отрезки 2 см и 3 см. Найдите эти отрезки.
Вариант 3
1. Катеты прямоугольного треугольника равны 15 см и 20 см, а в другом прямоугольном треугольнике гипотенуза и катет относятся как 5:3. Отношение периметров данных треугольников равно 5:1. Найдите стороны второго треугольника.
2. Дано: ABCD — трапеция; ∠ABC = ∠ACD; AD = 9 см; АС = 6 см. Найти: ВС.

3. Диагональ ромба делит его высоту, проведенную из вершины тупого угла, на отрезки длиной 5 см и 3 см. Найдите периметр ромба.
Вариант 4
1. Гипотенуза и катет прямоугольного треугольника равны 13 см и 12 см, а в другом прямоугольном треугольнике катеты относятся как 5:12. Отношение периметров данных треугольников равно 3:2. Найдите стороны второго треугольника.
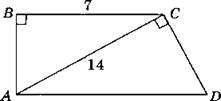
2. Дано: ABCD — прямоугольная трапеция; ∠ABC = ∠ACD = 90°; АС = 14 см; ВС = 7 см. Найти: AD.
3. Центр окружности, вписанной в равнобедренный треугольник, делит медиану, проведенную к основанию, на отрезки длиной 5 см и 4 см. Найдите периметр треугольника.