Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
ФУНКЦИИ y = x-1 И у = x-2 И ИХ СВОЙСТВА - СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ. ЭЛЕМЕНТЫ СТАТИСТИКИ
Цели: рассмотреть функции у = x-1 и у = х-2, изучить их свойства; формировать умения строить графики данных функций, решать задачи с их использованием.
Ход урока
I. Актуализация знаний.
Повторить свойства изученных ранее функций:
1. у = kх и частный случай у = х при k = 1.
2. у = хn, где n - натуральное число, в частности, у = х2 и у = x3 (знакомы из курса алгебры 7 класса).
3. ![]() и частный случаи
и частный случаи ![]() при k = 1.
при k = 1.
II. Объяснение нового материала.
1. Замечаем, что ![]() и перечисляем свойства функции у = х-1:
и перечисляем свойства функции у = х-1:
1) Если х > 0, то у > 0;
Если х < 0, то у < 0.
Графиком функции является гипербола, расположенная в 1-й и 3-й четвертях координатной плоскости.
2) Противоположным значениям аргумента соответствуют противоположные значения функции; график функции у = х-1 симметричен относительно начала координат.
3) Если значения аргумента при х > 0 неограниченно возрастают (х → ∞), то соответствующие им значения функции убывают (у → 0). Если значения аргумента при х > 0 убывают, то есть стремятся к нулю (х → 0), то соответствующие значения функции неограниченно возрастают (у → ∞).
Можно предложить учащимся самостоятельно сделать аналогичные выводы для х < 0.
4) Значения аргумента и соответствующие им значения функции являются взаимно обратными числами.
2. Замечаем, что ![]() и перечисляем свойства функции y = х-2:
и перечисляем свойства функции y = х-2:
1) При любом значении аргумента значения функции - положительные числа.
2) Любым противоположным значениям аргумента соответствуют равные значения функции; график функции у = х-2 симметричен относительно оси у.
3) Если х → +∞ или х → -∞, то у → 0;
если х → 0, то у → +∞.
4) График функции состоит из двух ветвей (плавных кривых), расположенных в 1-й и 2-й четвертях координатной плоскости. Для его построения необходимо взять несколько значений х > 0, причём как 0 < х < 1, так и х ≥ 1, и вычислить соответствующие значения функции. Построив одну ветвь графика, вторую получаем отображением её относительно оси у.
III. Формирование умений и навыков.
№ 1062.
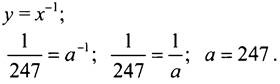
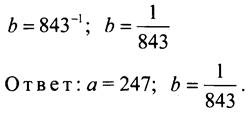
№ 1063.
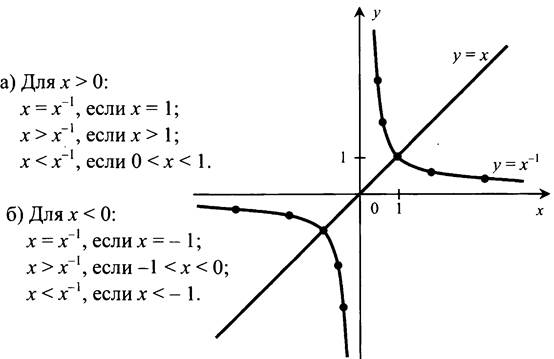
№ 1064.
![]()
Определим общие точки графиков, решив уравнение:
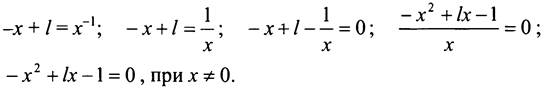
![]() - уравнение с параметром l.
- уравнение с параметром l.
![]()
1) Уравнение имеет 2 корня, если D > 0 (графики имеют две общие точки).
D > 0, если ![]() по свойству неравенств, l > 2.
по свойству неравенств, l > 2.
2) Уравнение имеет 1 корень, если D = 0 (графики имеют одну общую точку).
D = 0, если ![]() (так как l > 0).
(так как l > 0).
3) Уравнение не имеет корней, если D < 0 (графики не имеют общих точек).
D < 0, если ![]() по свойству неравенств l < 2.
по свойству неравенств l < 2.
№ 1068.
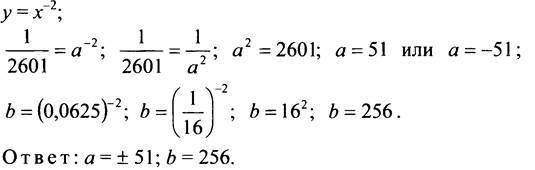
№ 1069.
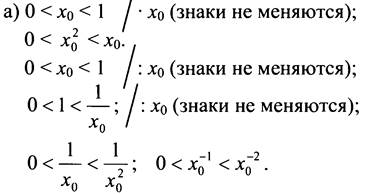
Имеем: ![]() значит, в порядке возрастания числа будут располагаться так:
значит, в порядке возрастания числа будут располагаться так:
![]()
б) Аналогично докажем, что при x0 > 1 в порядке возрастания числа будут располагаться так:
![]()
№ 1070.
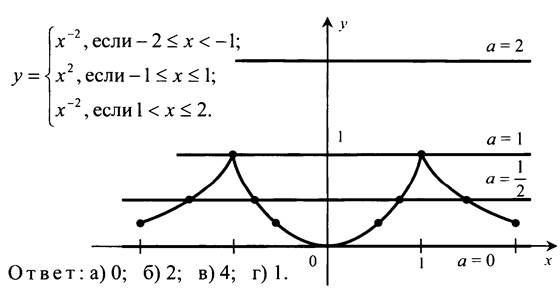
№ 1071.
Выполняем построение, аналогичное номеру 1070. Можно предложить выполнить дополнительное задание: определить, сколько корней имеет уравнение у = a? (а - параметр).
Уроки 99-101. ИТОГОВОЕ ПОВТОРЕНИЕ
Задания для итогового повторения курса алгебры 8 класса можно найти в дидактических материалах к учебнику.