Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
РЕШЕНИЕ ДВОЙНЫХ НЕРАВЕНСТВ - НЕРАВЕНСТВА
Цели: рассмотреть решение двойного неравенства через систему неравенств; продолжить формирование умения решать системы двух и более неравенств.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Решите систему неравенств:
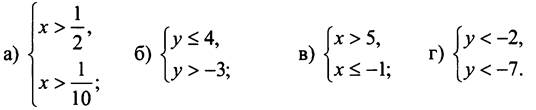
2. Известно, что 2 < х < 5. Оцените значение выражения:
а) 2х;
б) -х;
в) х - 3;
г) 3х - 1.
III. Объяснение нового материала.
1. На с. 187 рассмотреть пример 5.
Необходимо, чтобы учащиеся уяснили, что двойное неравенство представляет собой иную запись системы неравенств:
![]()
Решая систему, получим ![]() Полученное решение можно записать как в виде числового промежутка (-2; 0), так и в виде двойного неравенства -2 < х < 0.
Полученное решение можно записать как в виде числового промежутка (-2; 0), так и в виде двойного неравенства -2 < х < 0.
2. Двойное неравенство можно решать и другим способом, используя теоремы-свойства числовых неравенств:
- 1 < 3 + 2х < 3. Прибавляем к каждой части неравенства -3, получим:
-1 – 3 < 3 + 2х – 3 < 3 - 3
-4 < 2х < 0. Разделим каждую часть неравенства на 2, получим:
- 4 : 2< 2х : 2 < 0 : 2
-2 < х < 0.
IV. Формирование умений и навыков.
Все задания, решаемые на этом уроке, можно разбить на 4 группы:
1. Решение систем неравенств, содержащих дроби.
2. Решение двойных неравенств.
3. Решение систем трёх (и более) неравенств.
4. Решение заданий повышенной трудности.
1-я группа. № 890 (а, в), 891 (б, г).
№ 890.

№ 891.
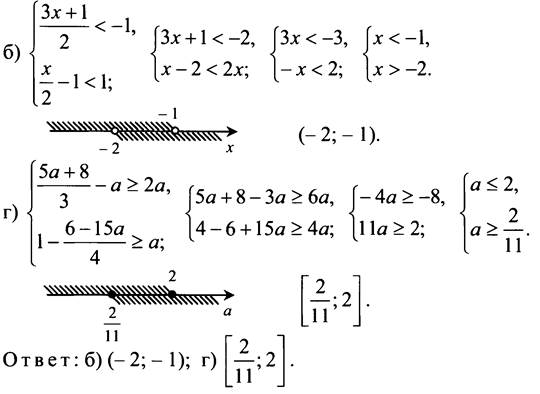
2-я группа. № 893(6; г), 894 (а; в), 895 (а).
№ 893.
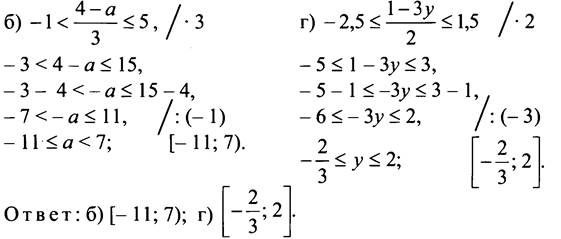
№ 894.
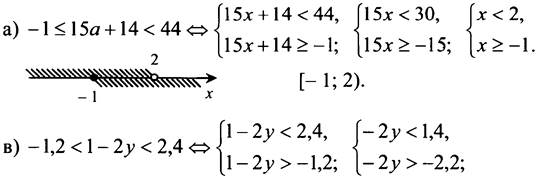
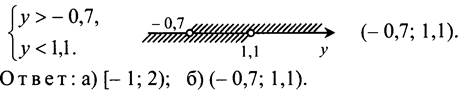
№ 895.
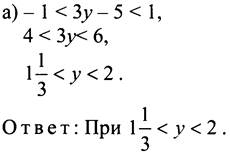
3-я группа. № 898 (а, в), 899 (б).
Обращаем внимание, что в системе три неравенства, значит, решением является пересечение трёх числовых промежутков.
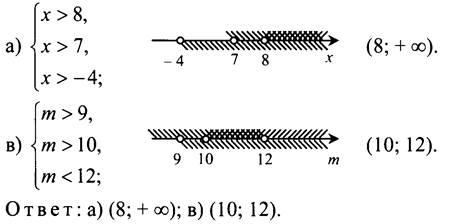
№ 898.
№ 899.
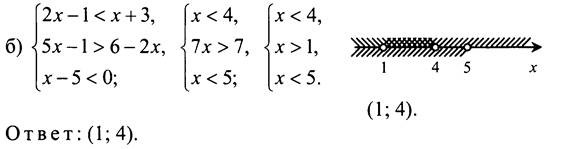
4-я группа (для сильных учащихся).
- При каких значениях а система неравенств ![]() не имеет решений?
не имеет решений?
Решение
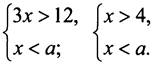 Чтобы система не имела решений, необходимо, чтобы (4; +∞) ∩ (-∞; а) = Ø.
Чтобы система не имела решений, необходимо, чтобы (4; +∞) ∩ (-∞; а) = Ø.
![]() Это верно, если а ≤ 4.
Это верно, если а ≤ 4.
Ответ: При а ≤ 4.
№ 896.
![]() - квадратное уравнение.
- квадратное уравнение.
![]() значит, уравнение имеет два различных корня. Найдём их:
значит, уравнение имеет два различных корня. Найдём их:
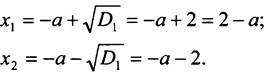
Так как оба корня должны принадлежать интервалу (-6; 6), то одновременно выполняются условия:
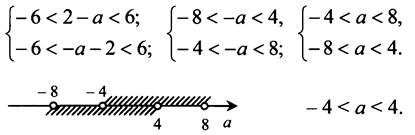
Ответ: при - 4 < а < 4.
V. Итоги урока.
- Что называется решением системы неравенств?
- Каков алгоритм решения системы неравенств?
- Какими способами можно решить двойное неравенство?
- В чём сущность решения системы, содержащей три и более неравенств?
Домашнее задание: № 891 (а), 895 (б), 900 (а), 889. Повторить п. 32-35 (подготовка к контрольной работе).