Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ПРОТИВОПОЛОЖНЫМИ ЗНАМЕНАТЕЛЯМИ - РАЦИОНАЛЬНЫЕ ДРОБИ
Цель: формировать умение складывать и вычитать рациональные дроби с противоположными знаменателями.
Ход урока
I. Организационный момент.
II. Устная работа.
Вычислите:
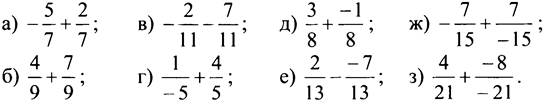
III. Объяснение нового материала.
Вспомните следствие из основного свойства дроби. Выполните задание, в котором нужно поменять знак числителя или знаменателя рациональной дроби.
![]()
Разбор примера 4 из учебника и формулирование вывода о том, как сложить или вычесть две рациональные дроби с противоположными знаменателями.
IV. Формирование умений и навыков.
1. Выполните сложение или вычитание дробей:

2. Выполните задания по учебнику: № 61, 63.
3. Преобразуйте выражение:
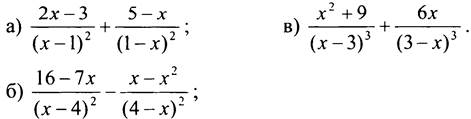
4. Выполните задания по учебнику: № 66, 68.
№ 68.
![]()
Полученное выражение принимает натуральные значения, если дробь 6/n является натуральным числом, то есть когда 6 делится на n. Значит, n = 1; 2; 3; 6.
Ответ: 1; 2; 3; 6.
V. Итоги урока.
-Сформулируйте правило сложения и вычитания рациональных дробей с одинаковыми знаменателями.
- Как выполнить сложение или вычитание рациональных дробей, знаменатели которых являются противоположными выражениями?
Домашнее задание: № 62, 64, 67, 69 (дополнительно).