Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ ВЫДЕЛЕНИЕМ КВАДРАТА ДВУЧЛЕНА - КВАДРАТНЫЕ УРАВНЕНИЯ
Цель: ознакомить учащихся с приемом решения квадратного уравнения выделением квадрата двучлена.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Назовите коэффициенты квадратного уравнения:
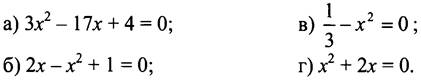
2. Найдите корни уравнения:

3. Представьте одночлен в виде удвоенного произведения двух множителей:
![]()
4. Разложите на множители:

III. Объяснение нового материала.
Для осознанного восприятия приёма решения квадратных уравнений путём выделения квадрата двучлена объяснение следует проводить в несколько этапов.
1. Актуализация знаний.
Прежде всего учащимся необходимо научиться свободно решать уравнения вида х2 = а и (х + k)2 = m.
Частично знания учащихся были актуализированы при выполнении устной работы. Чтобы ребята вспомнили, как решаются уравнения вида (х + k)2 = m, необходимо предложить им задание:
- Решите уравнение:
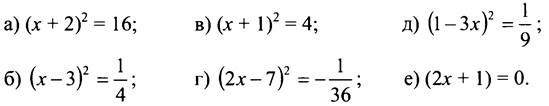
2. Ознакомление с приёмом решения квадратного уравнения путём выделения квадрата двучлена следует начать с рассмотрения приведённого квадратного уравнения, левая часть которого представляется в виде полного квадрата двучлена:
![]() и т. п.
и т. п.
После этого появляется возможность подвести учащихся к мысли о том, что для решения квадратного уравнения нужно привести его к виду (х + k)2 = m, а сделать это можно путём выделения квадрата двучлена. Сперва рассматриваем приведённое квадратное уравнение, одновременно выделяя алгоритм решения квадратных уравнений данным приёмом.
х2 - 6х - 7 = 0
1-й шаг. Записываем второй коэффициент в виде произведения двойки и некоторого числа: b = 2n.
х2 - 6х - 7 = х2 - 2 ∙ 3х - 7.
2-й шаг. Число п представляет собой второе слагаемое в искомом квадрате двучлена: n = 3. Для того, чтобы получить искомый квадрат двучлена (х - n)2 = х2 – 2 ∙ х ∙ n + n2, необходимо прибавить n2 и одновременно вычесть его:
![]()
3-й шаг. Выделяем квадрат двучлена:
![]()
4-й шаг. Решаем полученное уравнение, равносильное исходному:
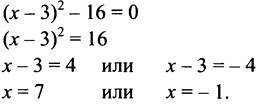
Ответ: -1; 7.
3. Решение неприведённых квадратных уравнений приёмом выделения квадрата двучлена.
Целью рассмотрения приёма решения квадратных уравнений путём выделения квадрата двучлена является подготовка к осознанному восприятию вывода общей формулы корней. Поэтому не стоит заострять внимание учащихся на технически сложных заданиях. Однако нужно рассмотреть со всем классом пример решения неприведённого квадратного уравнения указанным приёмом (с. 116-117 учебника).
IV. Формирование умений и навыков.
Следующие упражнения представляют собой последовательность квадратных уравнений, решаемых приёмом выделе ния квадрата двучлена, от простых к более сложным.
1. Решите устно.
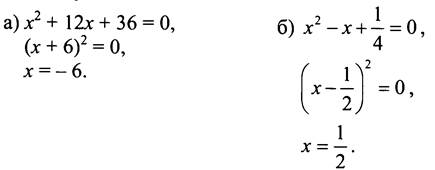

Уравнение не имеет решений.
Ответ: нет корней.
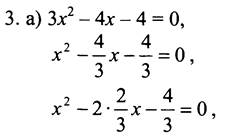
3. а) Зх2 - 4х - 4 = 0,
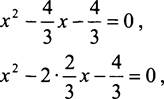
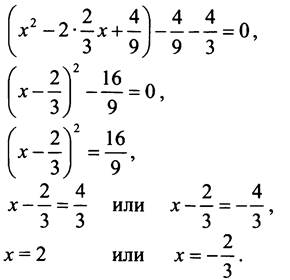
Ответ: -2/3; 2.
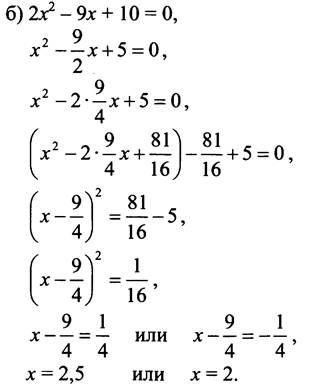
Ответ: 2; 2,5.
4. а) При каком значении а уравнение х2 - ах + 9 = 0 имеет ин корень?
Решение
Выделим квадрат двучлена.
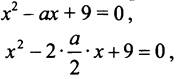
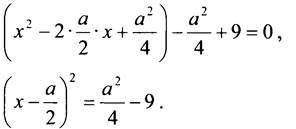
Это квадратное уравнение имеет единственный корень, если
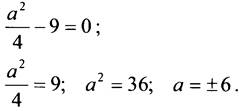
Ответ: при а = ±6.
б) При каком значении т уравнение 3х2 - mх - 6 = 0 имеет единственный корень?
Решение
Выделим квадрат двучлена.
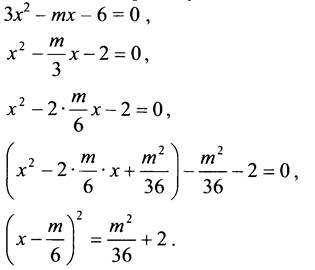
Это квадратное уравнение имеет единственный корень, если
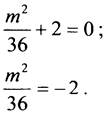
2
m2 = -72 - нет корней.
Ответ: нет решений.
V. Итоги урока.
- Какое уравнение называется квадратным?
- Какое квадратное уравнение называется приведённым?
- Как преобразовать неприведённое квадратное уравнение в приведённое?
- В чём заключается приём решения квадратных уравнений путём выделения квадрата двучлена?
- Любое ли квадратное уравнение может быть решено указанным приёмом?
Домашнее задание:
1. Решить методом выделения квадрата двучлена:
а) 5x2 + 3х - 8 = 0;
б) х2 - 8х - 9 = 0;
2. При каких значениях п можно представить в виде квадрата двучлена выражение:
а) х2 – nх + 16;
б) nх2 - 12х + 4?
3. Выполнить задания по учебнику: № 534 (б, г, д), 653 (а).