Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
РЕШЕНИЕ РАЗЛИЧНЫХ ЗАДАЧ, СВЯЗАННЫХ С ПРЕОБРАЗОВАНИЕМ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ КВАДРАТНЫЕ КОРНИ - КВАДРАТНЫЕ КОРНИ
Цель: закрепить знания и умения учащихся по преобразованию выражений, содержащих квадратные корни.
Ход урока
I. Организационный момент.
II. Устная работа.
Приведите подобные слагаемые:
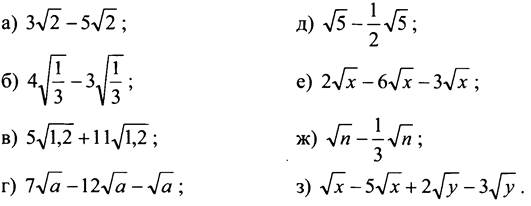
III. Формирование умений и навыков.
• Все задания можно разбить на две группы.
1-я группа. Более сложные, чем на предыдущем уроке, задания на преобразование выражений, содержащих квадратные корни: № 436 (а, в, д), 437, 435 (а, в), 434, 438.
№ 434.
а) Преобразуем данное выражение:
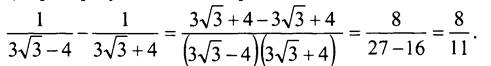
Таким образом, значение выражения является рациональным числом.
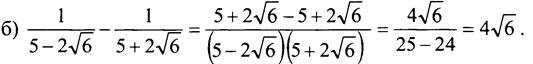
Таким образом, значение выражения является иррациональным числом.
№ 438.
Известно, что взаимно обратные числа в произведении дают единицу, а противоположные числа в сумме дают ноль.
![]() то есть данные числа являются взаимно обратными.
то есть данные числа являются взаимно обратными.
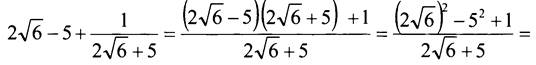
![]() то есть данные числа являются противоположными.
то есть данные числа являются противоположными.
2-я группа. Задания повышенного уровня сложности на преобразование выражений, содержащих квадратные корни: № 508, 511.
№ 508.
Сначала сократим данную дробь:
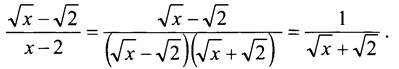
Так как выражение √x + √2 положительно при любых х, то дробь ![]() принимает наибольшее значение, когда её знаменатель наименьший. Выражение √х + √2 принимает наименьшее значение при х = 0.
принимает наибольшее значение, когда её знаменатель наименьший. Выражение √х + √2 принимает наименьшее значение при х = 0.
Ответ: при x = 0.
№ 511.
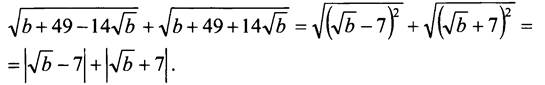
Выражение √b + 7 положительно при всех допустимых значениях b, поэтому ![]()
По условию 0 ≤ b ≤ 49; при таких значениях b выражение √b - 7 меньше либо равно нулю, поэтому ![]()
Таким образом, имеем:
![]() то есть исходное выражение не зависит от b.
то есть исходное выражение не зависит от b.
• Дополнительное задание. Докажите, что верно равенство:
![]()
Доказательство
Освободимся от иррациональности в знаменателе каждой дроби:
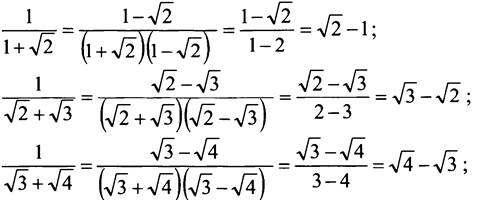
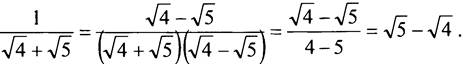
Преобразуем левую часть исходного равенства, подставляя в него полученные выражения:
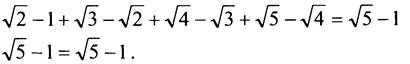
Равенство доказано.
IV. Итоги урока.
- Что называется арифметическим квадратным корнем из числа а?
- Сформулируйте все свойства арифметического квадратного корня.
- В чём состоит приём вынесения множителя из-под знака корня? внесения множителя под знак корня? Когда используются эти приёмы?
- Как освободиться от иррациональности в знаменателе дроби?
Домашнее задание: № 435 (б, г), № 436 (б, г, е), № 439, 506 (в, г) (дополнительно).