Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
ФУНКЦИЯ у = k/x И ЕЕ ГРАФИК В РЕШЕНИИ РАЗЛИЧНЫХ ЗАДАЧ - РАЦИОНАЛЬНЫЕ ДРОБИ
Цель: продолжить формирование умения использовать понятие, свойства и график функции ![]() при решении различных задач.
при решении различных задач.
Ход урока
I. Организационный момент.
II. Устная работа. Даны функции:
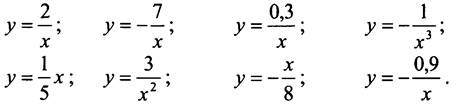
Среди таких функций найдите те, которые:
а) расположены в I и III координатных четвертях;
б) расположены во II и IV координатных четвертях;
в) положительны на промежутке (0; +∞);
г) отрицательны на промежутке (0; +∞).
III. Проверочная работа.
Вариант 1
Дана функция ![]()
1) Найдите значение у, соответствующее значению х, равному 2; 8; -1; -7.
б) Найдите значение х, которому соответствует значение у, равное 2; - 1; - 8.
в) Постройте график этой функции.
г) Укажите, при каких значениях х функция принимает положительные значения.
Вариант 2
Дана функция ![]()
а) Найдите значение у, соответствующее значению х, равному 2; 8; - 3; - 9.
б) Найдите значение х, которому соответствует значение у, равное - 3; 1; 12.
в) Постройте график этой функции.
г) Укажите, при каких значениях х функция принимает положительные значения?
IV. Формирование умений и навыков.
• № 183, 190 (в), 191, 186 (а), 187.
• В классе с высоким уровнем подготовки можно выполнить несколько дополнительных заданий, связанных с использованием графика функций ![]() при решении уравнений.
при решении уравнений.
№ 188.
Проиллюстрируйте каждый из случаев.
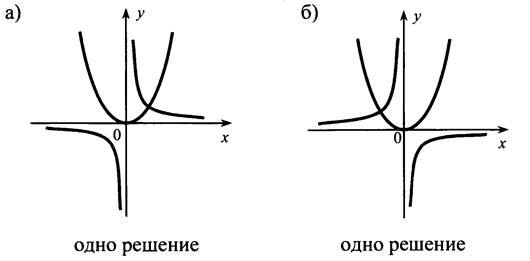
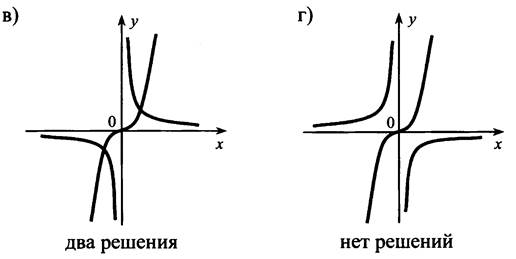
№ 261.
Если ответ на вопрос будет положительным, то необходимо показать его на рисунке.
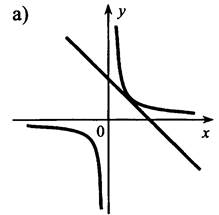
Графики функций ![]() и у = kх + b могут пересекаться только в одной точке. В этом случае прямая касается одной из ветвей гиперболы.
и у = kх + b могут пересекаться только в одной точке. В этом случае прямая касается одной из ветвей гиперболы.
Прямая может пересекать гиперболу в двух точках.
в) Прямая не может пересекать гиперболу в трёх точках. Это утверждение можно доказать, решая соответствующее уравнение: ![]()
Преобразовав это уравнение, получим квадратное уравнение ах2 + bх - k = 0, которое не может иметь более двух корней.
Значит, графики функций ![]() и у = kх + b не могут пересекаться в трёх точках.
и у = kх + b не могут пересекаться в трёх точках.
Найдите координаты какой-нибудь точки, принадлежащей графику функции у = 5/x и находящейся от оси x на расстоянии, меньшем, чем 0,1.
Решение
Сначала необходимо изобразить схематически график функции у = 5/x и прямые у = 0,1 и у = -0,1, поскольку точки, находящиеся от оси х на расстоянии 0,1, лежат на этих прямых.
Прямые у = 0,1 и у = — 0,1 пересекут ветви гиперболы в точках Aw В, которые находятся от оси х на расстоянии, равном 0,1. Очевидно, что все точки на гиперболе, расположенные правее точки А, будут ближе к оси х, значит, находятся на расстоянии, меньшем 0,1. То же самое можно сказать обо всех точках гиперболы, находящихся левее точки В.
Найдем абсциссу точки А: 0,1 = 5/x, откуда x = 50.
Таким образом, для нахождения искомых точек можно брать те точки, абсциссы которых больше 50. Аналогично получаем, что для левой ветви гиперболы такими точками будут те, абсциссы которых меньше - 50.
V. Итоги урока.
- Как называется функция ![]() ? Что является ее графиком?
? Что является ее графиком?
- В каких четвертях расположен график функции ![]() ?
?
- Какова область определения функции ![]() ?
?
Домашнее задание: № 186 (б), 189, 190 (б), 262 (дополнительно).