Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ у = k/x - РАЦИОНАЛЬНЫЕ ДРОБИ
Цели: ввести понятие функции обратная пропорциональность; формировать умение строить график этой функции.
Ход урока
I. Организационный момент.
II. Устная работа.
Выразите из формулы величину х:

III. Объяснение нового материала.
1. Введение функции обратная пропорциональность (рассмотрение реальных процессов и ситуаций).
Пример 1. Пешеходу надо пройти 12 км. Если он будет идти со скоростью V км/ч, то зависимость времени t, которое он затратит на весь путь, от скорости движения выражается формулой ![]()
Пример 2. Площадь прямоугольника равна 60 см2, а одно из его измерений равно а см. Тогда второе измерение можно найти по формуле ![]()
Пример 3. Количество товара m, которое можно купить на одну и ту же сумму денег в 500 р., зависит от его стоимости Р (в рублях). Эта зависимость выражается формулой ![]()
Полученные в примерах формулы выносятся на доску:
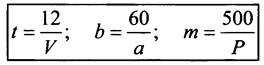
- Что общего имеют все данные формулы? Запишите полученные зависимости в общем виде: ![]() .
.
Заметить, что в данной формуле величины находятся в обратно пропорциональной зависимости, поэтому функцию ![]() называют обратной пропорциональностью.
называют обратной пропорциональностью.
На доску выносится запись:
Функция, заданная формулой вида ![]() , где k ≠ 0, называется обратной пропорциональностью.
, где k ≠ 0, называется обратной пропорциональностью.
Задание. Укажите, какие из функций являются обратной пропорциональностью.
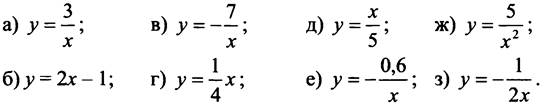
2. График функции ![]() .
.
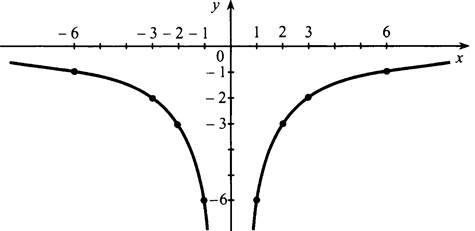
Построим график функции у = 12/x. По этому графику опишем некоторые свойства функции. Затем построим график функции у = -12/x и сопоставим его с графиком функции у = 12/x.
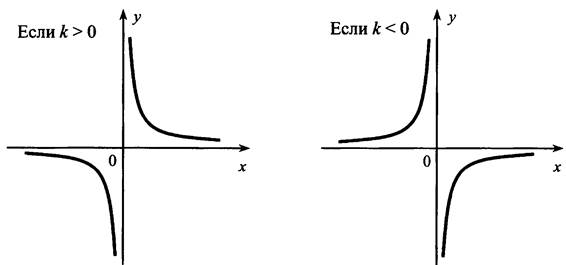
Сделаем вывод о расположении гиперболы в зависимости от коэффициента k (№ 192). Занесем в тетрадь следующую иллюстрацию:
Функция ![]()
График – гипербола
IV. Формирование умений и навыков.
• Выполнение заданий: № 179, 182, 185, 181.
• Дополнительное задание. Графиком какой из функций ![]() является гипербола? Постройте эту гиперболу.
является гипербола? Постройте эту гиперболу.
• Задание для сильных учащихся: № 257 (а, д).
а) Для построения графика функции ![]() необходимо рассмотреть два случая. При х > 0 данная функция совпадает с функцией
необходимо рассмотреть два случая. При х > 0 данная функция совпадает с функцией ![]() а при х < 0 - с функцией
а при х < 0 - с функцией ![]() Поэтому получим график
Поэтому получим график
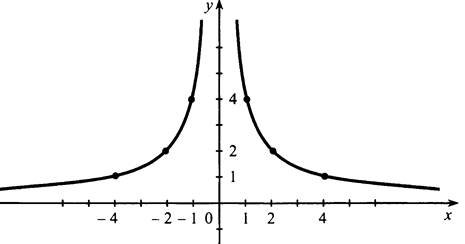
д) ![]() Рассуждая аналогично, получим график:
Рассуждая аналогично, получим график:
- Функция какого вида называется обратной пропорциональностью?
- Что является графиком функции ![]() ?
?
- В каких координатных четвертях расположен график функции ![]() в зависимости от л?
в зависимости от л?
- Какова область определения функции ![]() ?
?
Домашнее задание: № 180, 184, 193, 257 (б, г) (дополнительно).