Упрощение выражений - Урок 4 - УМНОЖЕНИЕ И ДЕЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ - НАТУРАЛЬНЫЕ ЧИСЛА

Основная дидактическая цель урока: продолжить работу по формированию умения упрощать выражения; познакомить с решением задач на части.

Ход урока

I. Организационный момент

II. Устный счет. Определение темы урока

На доске:

— Найдите значения выражений удобным способом.

— Какие свойства умножения вы использовали при вычислениях?

— Подумайте, можно ли использовать эти свойства при упрощении данного выражения.

4 ∙ а ∙ 6

— Объясните свое решение.

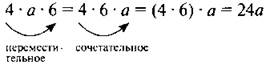
Сегодня на уроке будем выполнять упрощение таких выражений и познакомимся с решением задач нового типа.

III. Работа по теме урока

1.С. 88, № 575.

2. С. 88, № 576.

— Прочитайте задание.

— Рассмотрите левые части уравнений.

— Что необходимо сделать перед началом решения?

— На основе каких свойств будем упрощать левую часть?

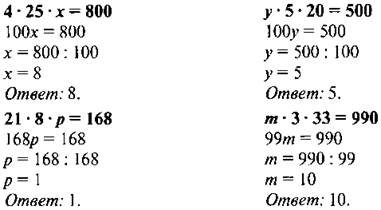
IV. Работа над задачами

1. С. 88, № 583.

— Прочитайте задачу.

— Это задача на части? Прочитайте объяснение ее решения. Обратите внимание на то, что в таких задачах принимают за х.

— Что же следует обозначить за х?

2. С. 89, № 585.

— Прочитайте задачу.

— Можно ли сказать, что эта задача на части?

— Какие компоненты необходимо взять для приготовления раствора?

— Сколько частей каждого компонента надо взять?

(В ходе анализа данных на доске появляется схема с кратким условием.)

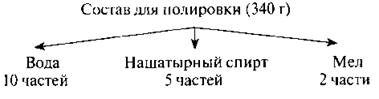
— Что следует обозначить за х?

Пусть масса одной части будет х.

Тогда масса воды будет 10х.

Масса нашатырного спирта будет 5х.

Масса мела будет 2х.

Масса всего состава будет 10х + 5х + 2х.

В условии сказано, что масса состава 340 г.

Значит, можем составить уравнение:

10х + 5х + 2х = 340

17х = 340

х = 340 : 17

х = 20 (г) — масса одной части.

10х = 20 ∙ 10 = 200 (г) — воды.

5х = 20 ∙ 5 = 100 (г) — нашатырного спирта.

2х = 20 ∙ 2 = 40 (г) — мела.

3. С. 89, № 586.

— Прочитайте задачу.

— Это задача на части?

— Какие компоненты берут для изготовления бутылочного стекла?

— Прочитайте вопрос задачи.

— Чем эта задача отличается от предыдущей?

— Что обозначим через х?

Пусть масса одной части будет х, тогда масса песка 25х. Масса соды будет 9х.

Масса извести будет 5х.

Общая масса стекла составляет 25х + 9х + 5х.

По условию задачи масса стекла 390 кг.

Значит, можем составить уравнение:

25х + 9х + 5х = 390

39х - 390 х = 390 : 39

х = 10 (кг) — масса одной части.

9х = 10 ∙ 9 = 90 (кг) — масса соды.

V. Самостоятельная работа

— Решите задачу с помощью уравнения.

Вариант 1

Масса двух чемоданов 20 кг. Масса одного из них в три раза больше массы другого. Найдите массу каждого чемодана. (5 кг и 15 кг.)

Вариант 2

Длина двух кусков провода 60 м. Длина одного куска в 5 раз больше длины другого. Найдите длину каждого куска провода. (10 м и 50 м.)

VI. Рефлексия

— Что бы вы хотели повторить на следующем уроке, почему?

— С какими задачами мы сегодня познакомились?

— Что следует обозначать буквой в этих задачах?

Домашнее задание

С. 92, № 621, 625 (а).