Поурочные разработки по Математике 5 класс к УМК Н.Я. Виленкина
Микрокалькулятор - Урок 2 - ИНСТРУМЕНТЫ ДЛЯ ВЫЧИСЛЕНИЙ И ИЗМЕРЕНИЙ - ДРОБНЫЕ ЧИСЛА
Основная дидактическая цель урока: учить выполнять вычислительные операции на калькуляторе; совершенствовать вычислительные навыки; продолжить работу над текстовыми задачами.
Ход урока
I. Организационный момент
II. Устный счет
1. Найдите.
На доске:

2. Решите задачу.
Сколькими разными способами можно разместить в дискетнице с шестью отделениями 6 дискет? (6!)
III. Определение темы урока
1. Отгадайте загадку и сформулируйте тему урока.
Этот друг надежен очень,
Мал, удобен, быстр и точен.
Думать много не заставит.
Занятые сам расставит. (Микрокалькулятор.)
2. Прочитайте: 452; 162; 782; 312; 572; 992.
— На микрокалькуляторе легко и быстро можно возвести число в квадрат. Это выполняется по такой программе:
![]()
— Обратите внимание: сразу после клавиши “умножение” нажимается клавиша “равно”.
3. Вычислите квадраты чисел.
![]()
На микрокалькуляторе можно возвести число и в куб, и в четвертую степень и т. д. Например, чтобы возвести число в четвертую степень, надо нажать на клавишу “равно” 3 раза, в пятую степень — 4 раза, в шестую степень — 5 раз и т. д.
IV. Работа по теме урока
С. 234, № 1540 (а—д, ж, з) (работа в паре).
— Составьте программу вычисления для первого выражения. (Следует обратить внимание учащихся на то, что не надо нажимать клавишу “равно” после первого выполненного действия в выражении с двумя действиями и т. д.)
Проверка
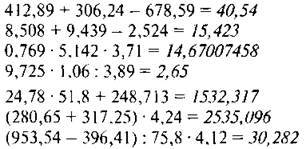
V. Повторение изученного материала
1. С. 234, № 1542 (работа в паре).
— Вычислите устно.
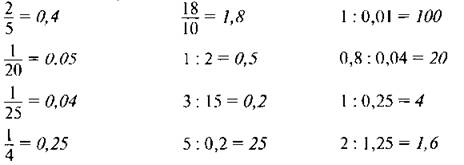
2. С. 235, № 1552.
— Какова средняя скорость движения поезда?
— С какой скоростью он шел первые 4 ч?
— Что еще известно в задаче?
— Что нужно узнать в задаче?
(В ходе анализа условия задачи составляется таблица.)
Скорость, км/ч
Время, ч
Расстояние, км
59,5
4
?
?
3
?
Средняя скорость на всем участке пути 67 км/ч.
(Полезно рассмотреть арифметический и алгебраический способы решения.)
— Что нужно узнать в задаче?
— Что для этого надо знать?
— Что нужно знать для того, чтобы найти второй отрезок пути? (Все расстояние и протяженность первого отрезка.)
— Как узнать весь путь?
— Как найти протяженность первого отрезка?
— Составьте план решения задачи.
— Решите задачу.
Арифметический способ решения
1) 4 + 3 = 7 (ч) — все время движения.
2) 67 ∙ 7 = 469 (км) — весь путь.
3) 59,5 ∙ 4 = 238 (км) — протяженность первого отрезка пути.
4) 469 — 238 = 231 (км) — протяженность второго отрезка пути.
5) 231 : 3 = 77 (км/ч) — скорость на втором отрезке пути.
Алгебраический способ решения
— Что следует обозначить за х?
— К чему будем приравнивать, составляя уравнение?
Пусть скорость на втором отрезке пути будет х.
Найдем среднюю скорость движения: (59,5 ∙ 4 + 3х) : (4 + 3).
В условии сказано, что средняя скорость равна 67 км/ч. Значит, можем составить уравнение:
(59,5 ∙ 4 + 3х) : (4 + 3) = 67
(238 + 3х) : 7 = 67
238 + 3х = 67 ∙ 7
238 + 3х = 469
3х = 469 - 238
3х = 231
х = 231 : 3
х = 77 (км/ч) — скорость на втором участке пути.
— Какое решение вам понравилось больше?
— Почему?
3. С. 235, № 1545 (работа в паре).
Проверка
1) 40 ∙ 3 = 120 (км) — первый отрезок пути.
2) 120 + 60 = 180 (км) — весь путь.
3) 3 + 1 = 4 (ч) — время движения.
4) 180 : 4 = 65 (км/ч) — средняя скорость движения.
4. С. 235, № 1549 (самостоятельно).
1) 70 + 90 = 160 (км) — все расстояние.
2) 2 + 3 = 5 (ч) — время движения.
3) 160 : 5 = 32 (км/ч) — средняя скорость теплохода.
VI. Рефлексия
— Что интересного узнали сегодня на уроке?
— Что понравилось?
Домашнее задание
С. 235, № 1556 (2-й столбик); с. 236, № 1560.