Вычисления с натуральными числами - Материалы для подготовки к самостоятельным работам

Пример 1. Вычислим:

а) 532 + 8936;

б) 7372 - 5147;

в) 5758 - 5689.

Решение.

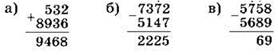
Пример 2. Вычислим:

а) 34 ∙ 73;

б) 5700 ∙ 36;

в) 543 ∙ 809.

Решение.

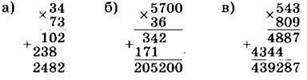
Пример 3. Вычислим:

а) 2880 : 45;

б) 21 744 : 36;

в) 164 500 : 47.

Решение.

Пример 4. Выполним деление с остатком и укажем остаток:

а) 5678 : 26;

б) 10 836 : 18;

в) 9876 : 77.

Решение.

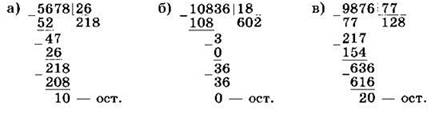
Пример 5. а) Найдём делимое m, если m : 21 = 7 (ост. 20).

б)Найдём делитель n, если 268 : n = 24 (ост. 4).

Решение.

а) Так как при делении m на 21 неполное частное равно 7, а остаток равен 20, то делимое m больше произведения 7 ∙ 21 на 20: m = 7 ∙ 21 + 20 = 167.

б) Если делимое 268 уменьшить на 4, то полученное число 268 - 4 = 264 разделится на n без остатка и частное будет равно 24, т. е. 264 : n = 24. Чтобы найти делитель n, делимое разделим на частное: n = 264 : 24 = 11.

Пример 6. Найдём наименьшее натуральное число, которое при делении на 7 даёт остаток 6, а при делении на 8 даёт остаток 1.

Решение.

I способ. Будем выписывать подряд натуральные числа, которые при делении на 8 дают остаток 1, а под ними будем писать остатки от деления этих чисел на 7. Как только остаток первый раз будет равен 6, то искомое число будет найдено:

Итак, наименьшее натуральное число, удовлетворяющее условию задачи, равно 41.

II способ. Любое натуральное число, которое при делении на 8 даёт остаток 1, можно записать в виде 8n + 1, где n = 0, 1, 2, 3, ... . Это число можно переписать в виде 7n + (n + 1). Остаток от деления этого числа на 7 равен 6 при n, равном 5, 12, 19 и т. д. Наименьшее из этих чисел равно 5.

Следовательно, наименьшее натуральное число, удовлетворяющее условию задачи, равно 8 ∙ 5 + 1 = 41.