Действие магнитного поля на движущийся заряд. Сила Лоренца - МАГНИТНОЕ ПОЛЕ - ОСНОВЫ ЭЛЕКТРОДИНАМИКИ

Задачи урока: выделить и изучить новое физическое явление — действие магнитного поля на движущуюся заряженную частицу; сформировать умение решать задачи на использование формулы для силы Лоренца.

План урока

Этапы урока	Время, мин	Приёмы и методы
I. Актуализация знаний II. Изучение нового материала: явление действия магнитного поля на заряженную частицу, закон этого действия. Применение знаний III. Отработка изученного материала IV. Подведение итогов. Домашнее задание	7—10 15—20 10—15 5	Решение задач. Фронтальный опрос Рассказ учителя. Демонстрация опытов. Работа с учебником Решение задач Фронтальное повторение. Запись на доске

I. В начале урока необходима актуализация знаний о силе Ампера. Один из школьников решает типичную задачу на доске. В это время организуют фронтальный опрос (возможен и диктант): какое физическое явление описывают силой Ампера? От чего зависит действие магнитного поля на ток? Что такое элемент тока? Как формулируется закон Ампера? Можно ли утверждать, что сила прямо пропорциональна вектору магнитной индукции? В каких случаях приведённая формула несправедлива? (Ответ. Магнитное поле неоднородно, проводник длинный и непрямолинейный, ток непостоянный.)

II. Рекомендуем следующую организацию изучения нового материала.

1. Учитель ставит учебную проблему: определить силу, действующую со стороны магнитного поля на движущуюся заряженную частицу. (В учебнике именно так, а не просто на заряд, который может рассматриваться как модель.) Идея получения формулы для силы Лоренца такова: нам известен закон Ампера, но электрический ток — это движущиеся заряженные частицы, отсюда сила Лоренца — это сила Ампера, действующая на ток, образованный движением одной заряженной частицы. Задание: с помощью учебника получить формулу для силы Лоренца.

2. Коллективно выполняют анализ полученной формулы с помощью ответов на вопросы: как направлена сила Лоренца (рис. 1.29 учебника)? Меняет ли она скорость заряженной частицы (рис. 1.30 учебника)? При каком движении заряженной частицы в магнитном поле сила Лоренца максимальна?

3. Учитель демонстрирует действие магнитного поля на движущиеся заряженные частицы: к электронно-лучевой трубке (или к экрану осциллографа при выключенной развёртке) подносят магнит, наблюдают отклонение луча (возможно использование специальной установки — ФЭ-1, с. 173). Вопросы для организации беседы: что представляет собой электронный луч? Каково направление движения положительного заряда? Как расположено внешнее магнитное поле? Предположите, как будет отклоняться на экране след электронного луча.

4. О применении закона и выражения для силы Лоренца лучше рассказать учителю. При этом используют рисунки циклотрона и масс-спектрографа (рис. 1.31 и 1.32 учебника).

III. Отработка изученного материала продолжается при решении задач. Типичную задачу подробно в процессе беседы решают на доске и в тетрадях.

Электрон движется в вакууме в однородном магнитном поле с индукцией 5 ∙ 10^-3 Тл. Скорость электрона равна 10⁴ км/с и направлена перпендикулярно линиям магнитной индукции. Определите силу, действующую на электрон, и радиус окружности, по которой он движется.

Анализ физического явления. В задаче рассматриваются два физических объекта — электрон и однородное магнитное поле. Поле не меняется, электрон движется. Кроме магнитного поля на электрон действует еще притяжение Земли, но этим действием мы пренебрегаем. (Как это доказать?)

Далее выполняют рисунок 9 и с его помощью уточняют представление о характере движения электрона. Это равноускоренное движение по окружности. Роль центростремительной силы играет сила Лоренца. При выполнении рисунка отмечают, что электрон моделируется материальной точкой.

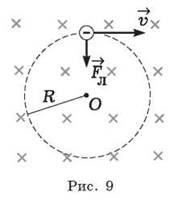
Идея решения заключается в использовании формулы для силы Лоренца и описании движения по окружности с помощью второго закона Ньютона.

Решение. Для угла 90° сила Лоренца вычисляется так:

Для нашего движения — движения материальной точки по окружности — записываем основное уравнение динамики:

В итоге получаем выражение для радиуса:

Анализ решения. Изменится ли решение, если принять, что линии вектора магнитной индукции направлены к нам? Как будет двигаться электрон в этом случае? Точные или приближенные значения силы и радиуса получены при решении задачи? (Ответ. Приближенные.) Почему? Вводилась ли при решении система отсчета?

IV. Домашнее задание: § 4; упр. на с. 23 (ЕГЭ); индивидуально — П., № 600.