Энергия связи атомных ядер - ФИЗИКА АТОМНОГО ЯДРА - КВАНТОВАЯ ФИЗИКА

Задачи урока: изучить диаграмму энергии связи атомных ядер, лежащую в основе выводов о поглощении или выделении энергии в ядерных реакциях; сформировать умение определять энергию связи.

Ход урока

I. Перед изложением нового материала следует повторить основные положения теории протонно-нейтронной модели ядра.

II. Какова основная характеристика такой физической системы, как ядро, — основная учебная проблема урока.

1. Изложение нового материала начинается с сопоставления ядра как системы нуклонов с атомом — системой ядра и электронов. Вспоминаем об энергии связи электрона в атоме: это энергия, которую нужно сообщить электрону, чтобы оторвать его от атома. Например, для атома водорода она равна 13,6 эВ (из основного состояния). Энергия связи электронов в оболочках многоэлектронных атомов составляет десятки и сотни электронвольт.

2. Энергией связи ядра атома называется энергия, необходимая для полного разделения ядра на нуклоны. Будем обозначать её E_св.

Энергия связи, приходящаяся на один нуклон, называется удельной энергией связи. Будем обозначать её е:

Понятно, что чем больше энергия связи, тем прочнее ядро.

Ядра не изменяются при химических реакциях, при поглощении света атомами потому, что энергия связи их много больше энергии, сообщаемой атомам в этих процессах.

Оказалось, что удельные энергии связи нуклонов в различных ядрах имеют значения от 2 до 9 МэВ (1 МэВ = 10⁶ эВ). Как же определить энергию связи? Формула для зависимости ядерных сил от расстояния точно неизвестна, неизвестно и точное расположение и движение нуклонов в ядре, поэтому рассчитать энергию связи ядра так, как это мы делали ранее для электрона в атоме, невозможно.

Зато благодаря большим энергиям связи можно для расчёта использовать формулу теории относительности:

Е = mc²,

где Е — энергия покоя частицы, a m — её масса покоя.

3. Как это сделать, рассмотрим на конкретном примере атома гелия. Протоны и нейтроны имеют массы

а масса ядра гелия

т. е. меньше суммы масс двух протонов и двух нейтронов на значение

Эта разность называется дефектом масс. С её помощью по формуле взаимосвязи массы и энергии вычисляем энергию связи:

Для гелия приближённо получаем

Осталось перевести это значение энергии в электронвольты:

На один нуклон приходится энергия

Такова удельная энергия связи ядра гелия.

Масса ядра гелия меньше суммы масс входящих в него нуклонов потому, что при соединении нуклонов в ядро ядерные силы притяжения совершают работу, при этом выделяется энергия взаимодействия, равная энергии связи. Она “уносит” часть массы покоя нуклонов. Если потребуется разъединить нуклоны ядра, то нужно затратить энергию, равную энергии связи (совершить работу против ядерных сил), восполнив тем самым энергию покоя и массы нуклонов до прежнего значения.

Энергия связи по изменённой массе ядра и известным массам протона и нейтрона рассчитывается для любого элемента по формуле

Измерения и расчёты проведены для всех элементов. Результаты этой большой работы учёных-физиков обобщены графически, построена диаграмма удельных энергий связи (рис. 12.1 учебника). С помощью этой важной диаграммы можно определить энергии всех ядерных превращений.

4. Оценим сначала по энергии связи значения ядерных сил, сравнивая их с электрическими. В теории атома рассматривалась формула энергии взаимодействия двух электрических зарядов. Она оказалась обратно пропорциональной расстоянию между зарядами. В электронной оболочке энергия связи порядка 10 эВ при расстоянии электрона от ядра 10^-10 м. Если перейти к расстоянию порядка 10^-14 м, то энергия связи увеличится в 10⁴ раз и будет порядка 10⁵ эВ.

Энергия же связи нуклонов в ядре, обусловленная действием ядерных сил, порядка 10 МэВ = 10⁷ эВ, т. е. в 100 раз больше. Значения ядерных сил считают превышающими значения электромагнитных в 100 раз.

5. Рассмотрим с помощью диаграммы (рис. 137), что произойдёт, если удастся соединить лёгкие ядра (начало периодической таблицы) и получить из них более тяжёлые. Поскольку энергия связи у ядер железа и близких к нему элементов наибольшая (≈ 9 МэВ), то при соединении ядер с меньшим числом нуклонов в ядра с большим числом нуклонов получим выделение энергии в несколько мегаэлектронвольт на каждый нуклон. (Заметим, что в пересчёте на макроскопическое количество вещества это очень большие энергии, так как атомы малы и в веществе их очень много.)

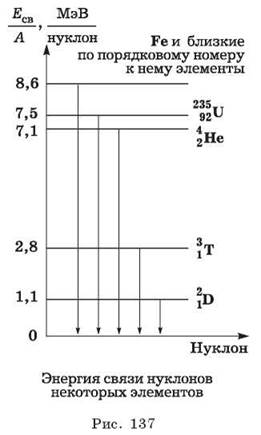
В качестве примера такого выделения энергии можно назвать реакцию соединения четырёх ядер водорода в ядро гелия (два протона при этом превращаются в нейтроны) с выделением энергии, как мы подсчитали, около 6,8 МэВ на один нуклон или около 27 МэВ на одно ядро образовавшегося гелия.

Другая возможность высвобождения ядерной энергии заключается в делении ядер элементов, находящихся в конце периодической таблицы. Из диаграммы видно, что если удастся разделить ядро урана на два ядра элементов, находящихся в середине таблицы, то на каждый нуклон высвободится энергии около 1 МэВ, всего на ядро урана около 200 МэВ.

Как реакции соединения ядер, так и реакции деления осуществлены человеком в наше время и используются для получения энергии.

III. Задачи на энергию связи могут быть составлены на основе диаграммы и справочных данных о ядрах.

1. Чему равна энергия связи ядра дейтерия — изотопа водорода ²₂H (тяжёлый водород)? Масса ядра дейтерия 3,34456 ∙ 10^-27 кг.

2. Работа по разделению молекулы воды на водород и кислород приблизительно равна 5 эВ. Оцените, во сколько раз атомные ядра прочнее молекулы воды.

3. Быстролетящий нейтрон проникает в ядро. Изменится ли при этом энергия связи ядра?

4. Рассчитайте энергию, выделяющуюся при превращении 1 г водорода в гелий.

5. Рассчитайте энергию, выделяющуюся при делении 1 г урана.

IV. Домашнее задание: § 80, 81* (3-5); упр. на с. 307 (ЕГЭ); упр. на с. 309 (4).