Механические свойства тел - ТВЕРДОЕ ТЕЛО

Цель урока: сформировать понятие упругость и пластическая деформация, научить решать задачи на закон Гука.

Ход урока

I. Повторение изученного. Проверка домашнего задания

1. На какие три вида по характеру относительного расположения частиц делятся твердые тела?

2. Чем определяется принадлежность твердых тел к одному из этих видов?

3. Чем характеризуется пространственное расположение частиц в критической решетке?

4. Какие точки называются узлами кристаллической решетки?

5. В чем отличие моно- и поликристаллов?

6. Перечислите основные типы кристаллических решеток.

7. Приведите пример полиморфизма.

8. Что такое анизотропия и изотропия?

9. Какие кристаллы анизотропные, а какие изотропны?

II. Изучение нового материала

Растяжение и сжатие приводят к деформации тела .Деформация тела - изменение его размеров или формы (сдвиги, изгибы, кручение).

При деформации возникает сила упругости, она направлена в сторону, противоположную направлению частиц тела при деформации. Но не всегда деформация приводит к появлению сил упругости. Пластичные тела не восстанавливают своей формы после прекращения действия силы.

III. Фронтальная лабораторная работа «Наблюдение упругих и пластических деформаций тел»

Приборы и материалы: 1) резина ученическая (ластик); 2) брусок металлический размером 40 х 25 х 8 мм; 3) брусок пластилиновый размером 30 х 20 х 8 мм.

Ход работы

1. Растяните, затем согните ластик.

2. Ответьте на вопросы:

- Как направлены силы, действующие на ластик при его растяжении и сжатии?

- Как направлена сила упругости, возникающая в ластике при деформации, относительно направления смещения его частиц?

- Как изменялись длина и площадь поперечного сечения ластика при его растяжении и сжатии?

- Восстанавливается ли форма ластика после снятия нагрузки?

3. Положите ластик на стол и прижмите его бруском. Перемещая брусок горизонтально, наблюдайте деформацию сдвига.

4. Ответьте на вопросы:

- Как направлены силы, действующие на ластик при деформации сдвига?

- Как смещались слои ластика относительно друг друга при деформации сдвига?

- Как изменялась деформация сдвига при увеличении нагрузки?

5. Изогните ластик. В каких слоях ластика возникли деформации растяжения, а в каких - сжатия?

6. Скрутите ластик. Из каких ранее рассмотренных деформаций состоит деформация кручения?

7. Подвергните деформации сжатия брусок из пластилина. Восстанавливается ли его форма после снятия нагрузки?

Виды деформации

1. Деформация растяжения. (Испытывают тросы, подъемные механизмы.)

При растяжении и сжатии изменяется площадь поперечного сечения. Эту деформацию характеризуют абсолютным удлинением Δl = l - l₀ и относительным удлинением

2. Деформация сдвига (подвержены заклепки, болты) характеризуется углом? (Абсолютная деформация.)

3. Деформация изгиба (балки и стержни, расположенные горизонтально). Деформацию изгиба можно свести к деформации неравномерного растяжения и сжатия.

4. Деформация кручения (валы машин, винты). Деформацию кручения рассматривают как неоднородный сдвиг.

В любом сечении деформированных тел действуют силы упругости, препятствующие разрыву тела на части. Тело находится в напряженном состоянии, которое характеризуется механическим напряжением:

Опыты показывают: при малых деформациях напряжение прямо пропорционально относительному удлинению: - закон Гука.

Е - модуль Юнга, характеризует сопротивляемость материала упругой деформации.

IV. Повторение изученного

1. Что такое деформация?

2. Какую деформацию называют упругой? Пластической?

3. Назовите виды деформаций.

4. Объясните, что происходит с телом при его растяжении и сжатии.

5. Что называют абсолютным удлинением тела? Какой формулой выражается смысл этого понятия?

6. Что называют относительным удлинением? Какая формула выражает смысл этого понятия?

7. В чем сходство и различие деформации сдвига и кручения?

8. Охарактеризуйте деформации изгиба. Почему в технике и в строительстве вместо стержней и сплошных брусьев применяют трубы, двутавровые балки, рельсы, швеллеры?

9. К какому виду деформации относится срез?

10. Что называют механическим напряжением? Какая формула выражает смысл этого понятия? Какова единица механического напряжения в СИ?

11. Каков физический смысл модуля упругости? Как следует понимать: модуль упругости стальной проволоки 2 · 10¹¹ Па, алюминия 7 · 10¹⁰ ПА?

12. 3апишите формулу закона Гука для одностороннего растяжения или сжатия и как она формулируется?

13. Что такое жесткость? Какова единица жесткости в СИ?

V. Решение задач

1. Проволока длиной 5,4 м под действием нагрузки удлинилась на 2,7 мм. Определить относительное удлинение проволоки.

Решение:

относительное удлинение проволоки: где Δl - абсолютное удлинение проволоки.

Отсюда

Относительное удлинение - величина безразмерная.

(Ответ: Е = 5 · 10^-4.)

2. Какова должна быть площадь поперечного сечения стального стержня, чтобы при нагрузке 25 кН растягивающее напряжение равнялось 6 · 10⁷ Па?

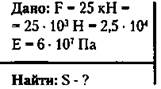
Решение:

По определению механического напряжения:

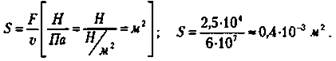
(Ответ: S ≈ 0,4 · 10^-3 м².)

3. На сколько удлинится медная проволока длиной 3 м и диаметром 0,12 мм под действием гири весом 1,5 Н? Деформацию считать упругой.

Решение: модуль упругости меди (т. е. модуль Юнга) определяем по таблице. Проволока удлинилась под действием гири, следовательно, вес гири равен силе, вызывающей деформацию проволоки. Воспользуемся законом Гука: V = Е · S, учитывая, что механическое напряжение Относительное удлинение проволоки и площадь поперечного сечения проволоки получим отсюда удлинение проволоки: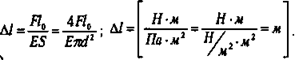

(Ответ: Δl = 3,3 мм.)

5. При какой предельной нагрузке разорвется стальной трос диаметром 1 см, если предел прочности стали 1 ГПа? (Ответ: F_np = 78,5 кН.)

6. Вычислите модуль упругости для железа, если известно, что железная проволока длиной 1,5 м и сечением 10^-6 м² под действием силы в 200 Н удлинилась на 1,5 мм. (Ответ: Е = 2 · 10¹¹ Па.)

7. Верхний конец стержня закреплен, а к нижнему подвешен груз 20 кН. Длина стержня 5 м, сечение 4 см². Определить напряжение материала стержня и его абсолютное и относительное удлинение, если модуль Юнга для этого стержня равен 2 · 10¹¹ Па. (Ответ: E = 5 · 10⁷ Па; Е = 2,5 · 10^-4; Δl = 1,25 мм.)

8. Найти площадь поперечного сечения алюминиевого прутка, к которому подвешена люстра массой 250 кг, при запасе прочности прутка 4. Предел прочности для алюминия 1,1 · 108 Па. Какова относительная деформация прутка? (Ответ: S = 8,9 · 10^-5 м²; Е = 3,93 · 10^-4.)

Домашнее задание

Прочитать конспект в тетради.