Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Ломаные, многоугольники
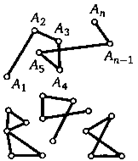
непростые ломаные простые ломаные
плоский
многоугольник
Ломаной называется набор точек на плоскости, последовательно соединенных отрезками3. Данные отрезки — звенья ломаной, а указанные точки —ее вершины. Например, ломаная А1А2А3...Ап состоит из отрезков А1А2, А2А3у ..., An_iAn. При этом ломаные А1А2А3... ...Ап и AnAn_1...A3A2^i мы будем считать одной и той же ломаной.
Ломаная называется замкнутой, если первая ее вершина совпадает с последней4.
Ломаная называется простой, если из каждой ее вершины выходит не более двух звеньев, а звенья не имеют общих точек, отличных от вершин.
Многоугольником называется простая замкнутая ломаная, соседние звенья которой не лежат на одной прямой.
Плоский многоугольник — это многоугольник вместе со своей внутренней областью5.
Диагональ многоугольника — отрезок, соединяющий две его вершины и отличный от стороны.
1. Какие цифры индекса (см. на конверте) являются простыми ломаными?

3 Отрезок—тоже ломаная, но имеющая только одно звено.
4 В случае, когда ломаная замкнута, любую ее вершину можно считать первой. Например, ломаные А1А2А3...Ап и A2A3...AnAi — это одно и то же.
5 То, что многоугольник разбивает плоскость на две области, — теорема. Но доказывать ее мы не будем. Внутренней областью многоугольника называют ту из областей, которая не содержит внутри себя ни одной прямой.
2. У простой ломаной 10 вершин. Сколько у нее может быть звеньев?
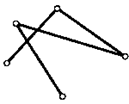
3. а) Сколько всего существует незамкнутых ломаных, соединяющих данные пять точек на рисунке (через каждую точку ломаная проходит только 1 раз)?
б) Тот же вопрос для замкнутых ломаных.
4. Нарисуйте самопересекающуюся замкнутую ломаную из шести звеньев, которая каждое свое звено пересекает ровно один раз.
5. Нарисуйте самопересекающуюся замкнутую ломаную из семи звеньев, которая каждое свое звено пересекает ровно два раза.
6. Соедините 16 точек на рисунке отрезками так, чтобы получился многоугольник (не забудьте, что у многоугольника соседние стороны не лежат на одной прямой!).
✵ • • •
✵ • • •
7. Могут ли четыре данные точки на плоскости быть вершинами разных четырехугольников?
8. Семь точек соединили отрезками так, что из каждой выходит ровно два отрезка. Обязательно ли они образуют замкнутую ломаную?
9. Сколько всего диагоналей у 20-угольника?
10. Число диагоналей многоугольника в четыре раза больше числа его сторон. Сколько у него вершин?
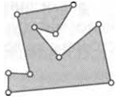
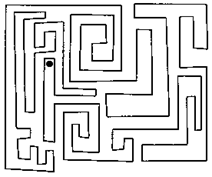
11. Во внутренней или во внешней области показанного на рисунке многоугольника находится отмеченная точка?
12. Может ли замкнутая пятизвенная ломаная разбивать плоскость на три различные области?
13. Прямая не проходит через вершины многоугольника. Докажите, что она пересекает его в четном числе точек.
14. Какое наибольшее число сторон может иметь фигура, являющаяся пересечением треугольника и четырехугольника?
15. Два многоугольника расположены так, что вершины каждого из них не принадлежат другому. Докажите, что они пересекаются в четном числе точек.