Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Применение площадей
1. Внутри выпуклого равностороннего многоугольника движется точка. Докажите, что сумма расстояний от нее до его сторон (или их продолжений) постоянна.
2. Катеты прямоугольного треугольника равны а и Ъ, а его гипотенуза — с. Найдите высоту треугольника, опущенную на гипотенузу.
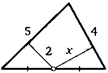
3. Две стороны треугольника равны 4 и 5. Расстояние от середины третьей его стороны до большей из них равно 2. Чему равно расстояние до меньшей стороны?
4. Стороны прямоугольного треугольника равны 6,8 и 10. Внутри него взяли точку на расстоянии 1 от каждого катета. Найдите расстояние от этой точки до гипотенузы.
5. Окружность касается катетов прямоугольного треугольника, а ее центр лежит на гипотенузе. Найдите радиус данной окружности, если катеты равны а и Ъ.
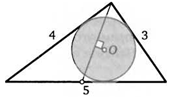
6. Прямоугольный треугольник со сторонами 3,4,5 называется египетским. Вне египетского треугольника взяли точку так, что расстояния от нее до продолжений его катетов равны 1 и 2 (см. рисунок). Найдите расстояние от этой точки до гипотенузы.
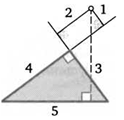
7. Стороны прямоугольного треугольника равны 3, 4 и 5. Найдите расстояние от центра его вписанной окружности до медианы, проведенной к гипотенузе.
8. (Лемма о пропорциональных отрезках.) Несколько параллельных прямых пересекают стороны угла. Докажите, что отношение отрезков, которые они высекают на одной стороне угла, равно отношению соответствующих отрезков на другой его стороне.
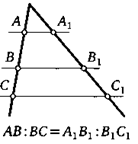
9. (Свойство биссектрисы треугольника.) Докажите, что биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
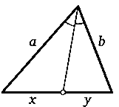
х/у=а/Ъ
10. Методом площадей докажите, что медианы треугольника пересекаются в одной точке.
11. (Замечательное свойство трапеции.)
а) Докажите, что середины оснований и точка пересечения диагоналей любой трапеции лежат на одной прямой.
б) Докажите, что на той же прямой лежит точка схода ее боковых сторон (пересечение их продолжений).
12. Отрезок, соединяющий середины противоположных сторон четырехугольника, проходит через точку пересечения его диагоналей. Верно ли, что это трапеция или параллелограмм?
13. Через точку пересечения диагоналей трапеции параллельно ее боковым сторонам провели две прямые. Первая из них пересекла одно ее основание в точке М, а вторая —другое основание в точке К. Докажите, что отрезок МК делит одну из диагоналей трапеции пополам.
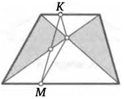
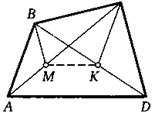
14. На сторонах АВ и ВС треугольника АВС взяты точки М и К, так что AM/МВ = 2/3, ВК/КС = 4/5. Через середину отрезка МК и вершину В провели прямую. В каком отношении она делит сторону АС?
В
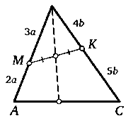
15. (Теорема Чевы.) а) Внутри треугольника АВС взяли произвольную точку О. Прямые АО, ВО и СО пересекают стороны ВС, АС и АВ в точках N, К и М соответственно. Докажите, что верно соотношение AM/ВЫ • BN/CN • СК /АК = 1.
б) Сформулируйте и докажите обратное утверждение.
В
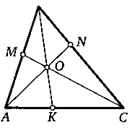
16. Вписанная в треугольник окружность касается его сторон в трех точках. Каждую из них соединили с противоположной вершиной. Докажите, что три полученных отрезка пересекаются в одной точке.
17. Используя теорему Чевы, еще раз докажите, что все биссектрисы треугольника пересекаются в одной точке.
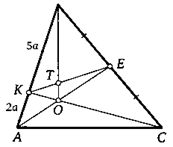
18. На стороне АВ треугольника АВС взяли точку К так, что АК :ВК = 2:5. Точка Е — середина стороны ВС. Отрезки АЕ и СК пересекаются в точке О, отрезки КЕ и ВО пересекаются в точке Г. Найдите КТ: ТЕ.
В
19. На диагоналях АС и BD выпуклого четырехугольника ABCD взяты такие точки М и К, что ВЫ параллельно CD, а СК параллельно АВ. Докажите, что отрезок МК параллелен AD.
С
20. Четыре диагонали пятиугольника соответственно параллельны четырем его сторонам. Докажите, что пятая диагональ пятиугольника также параллельна его стороне.
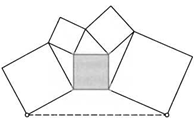
21. Квадраты расположены так, как показано на рисунке. Верно ли, что пунктирный отрезок всегда параллелен стороне «центрального» квадрата?
22. На клетчатой бумаге нарисовали многоугольник, вершины которого лежат в узлах, а стороны не проходят по ее линиям. Докажите, что сумма всех горизонтальных отрезков сетки, заключенных внутри многоугольника, равна сумме всех вертикальных.

23. В треугольнике АВС взяли произвольную точку М. Прямые AM, ВЫ и СМ пересекают стороны в точках Аъ В1иС1. Докажите, что MA1/AAl-^MBl/BBl -hMCjCCj = 1.
Формула для площади описанного многоугольника
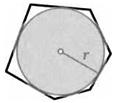
24. (Формула для площади описанного многоугольника.)
Многоугольник описан вокруг окружности с радиусом г. Докажите, что его площадь можно вычислять по формуле S = рг, где р — половина периметра многоугольника.
S = р - г
25. Высоты треугольника равны 3, 4 и 5. Найдите радиус его вписанной окружности.
26. Радиус вписанной окружности треугольника равен 1, а высота, опущенная на его основание, равна 3. Найдите радиус окружности, касающейся его боковых сторон, центр которой находится на основании треугольника.
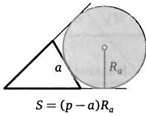
27. Докажите, что площадь треугольника можно вычислять по формуле S = Ra(p — a), где р — половина периметра треугольника, a Ra — радиус вневписанной окружности, касающейся стороны а.
28. Высота, опущенная на основание треугольника, равна радиусу вневписанной окружности, касающейся этой стороны. Докажите, что основание равно среднему арифметическому двух других сторон треугольника.
29. Пусть г —радиус вписанной окружности треугольника, а Ra, Rbi Rc — радиусы его вневписанных окружностей. Докажите, что l/r = l/Ra + 1/Rb + 1/RC.
30. Прямая делит одну боковую сторону треугольника на отрезки с длинами 5 и 1, а другую — на отрезки с длинами 4 и 3, считая от общей вершины. Найдите основание треугольника, если известно, что на данной прямой лежит центр вписанной в треугольник окружности.
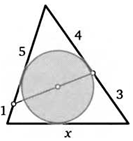
31. Стороны треугольника равны 4, 5 и 6. Через середину его большей стороны и центр вписанной окружности провели прямую. В каком отношении она делит другую сторону треугольника?
32. Некоторая прямая делит площадь и периметр треугольника пополам. Докажите, что все такие прямые пересекаются в одной точке.
1
Подумайте, почему условие выпуклости четырехугольника существенно.
2
По сути можно сказать, что площадь — это числовая функция, заданная на множестве плоских фигур и удовлетворяющая четырем указанным аксиомам.