Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Вписанные углы
Дуга
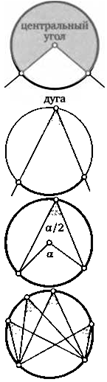
Любые два луча, выходящие из центра окружности, делят ее на две части. Каждая из этих частей называется дугой окружности. Два плоских угла, образованных данными лучами, называют центральными. Величина центрального угла, определяющего данную дугу, называется градусной мерой дуги.
Угол называется вписанным в окружность, если его вершина лежит на окружности, а стороны пересекают окружность.
Говорят, что вписанный угол опирается на дугу окружности, если его стороны проходят через концы этой дуги, а вершина не принадлежит дуге.
Теорема о вписанном угле. Величина вписанного в окружность угла равна половине градусной меры дуги, на которую он опирается.
Из данной теоремы следует, что все углы, вписанные в одну окружность и опирающиеся на одну дугу, равны.
Свойство ВПИСАННОГО ЧЕТЫРЕХУГОЛЬНИКА. Сумма противоположных углов вписанного четырехугольника равна 180°.
1. Верно ли такое определение вписанного угла: угол называется вписанным в окружность, если он имеет с ней ровно три общие точки?
2. В одну окружность вписаны два равных угла. Докажите, что они опираются на равные хорды. Верно ли обратное?
3. Трапеция вписана в окружность. Докажите, что она равнобокая.
4. В окружности проведена хорда, равная ее радиусу. Какова может быть величина угла, вписанного в эту окружность и опирающегося на данную хорду?
5. В окружность вписали шестиугольник ABCDEF. Оказалось, что в нем AD || ВС, CF || DE. Докажите, что тогда BE || AF.
В
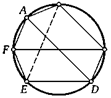
6. Пятиугольник вписан в окружность. Один его угол равен 150°, а три стороны, не выходящие из вершины данного угла, равны между собой. Найдите угол а между этими сторонами.
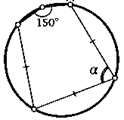
7. В треугольнике провели две высоты. Их продолжения пересекают его описанную окружность в двух точках. Докажите, что эти точки равноудалены от третьей вершины треугольника.
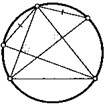
8. Пусть О — центр описанной окружности треугольника ЛВС, АН — его высота. Докажите, что АВАН — АОАС.
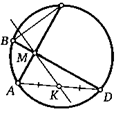
9. В круге через точку М провели две перпендикулярные хорды АС и BD. Точка К — середина отрезка AD. Докажите, что прямые МК и ВС перпендикулярны.
10. Основание АС равнобедренного треугольника ЛВС является радиусом окружности. Продолжения боковых сторон треугольника пересекают окружность в точках D и Е. Прямые DE и АС пересекаются в точке М. Докажите, что AM = АЕ.
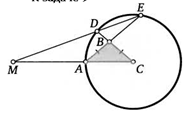
11. Точка О — центр описанной окружности треугольника АВС. Точка / — центр вписанной в него окружности. Известно, что ААОС — 60°. Найдите ZAIC. Внимание: задача имеет 2 решения!
12. На основании равнобедренного треугольника взяли произвольную точку. Отрезок, соединяющий ее с противоположной вершиной, делит треугольник на два меньших треугольника. Докажите, что радиусы окружностей, описанных вокруг этих треугольников, равны.
13. Хорды АВ и CD одной окружности пересекаются в точке М. Найдите угол АМС, если градусные меры дуг АС и BD равны а и Р соответственно. Сформулируйте и докажите аналогичное утверждение для случая, когда прямые АВ и CD пересекаются вне круга в точке М.
а
А
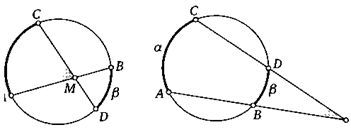
М
14. Две окружности пересекаются в точках Л и Б. На одной из них берется произвольная точка М. Прямые МА и МВ пересекают вторую окружность в точках Р и Q. Докажите, что длина хорды PQ не зависит от выбора точки М.
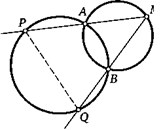
М
15. В окружность вписан равносторонний десятиугольник АгА2...А10. Найдите угол между прямыми: а) АгА7 и А4А9; б) А7А8 И А3А5.
16. Биссектрисы двух углов треугольника пересекают описанную вокруг него окружность в точках М и К. Докажите, что отрезок МК перпендикулярен биссектрисе третьего угла треугольника.
17. Докажите свойство вписанного в окружность четырехугольника.
18. Шестиугольник вписан в окружность. Найдите сумму углов при трех его не соседних вершинах.
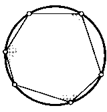
19. Найдите сумму четырех аналогичных углов для вписанного в окружность восьмиугольника.
20. Во вписанном четырехугольнике равны два угла при соседних вершинах. Докажите, что у него есть две параллельные стороны.
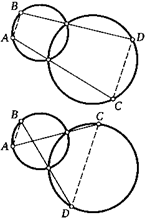
21. Через точки пересечения двух окружностей проведены две произвольные прямые. Они пересекают первую окружность в точках Л и В, а вторую — в точках С и D. Докажите, что АВ || CD (разберите два случая).
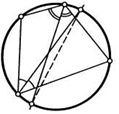
22. Биссектрисы противоположных углов вписанного в окружность четырехугольника пересекают ец в двух точках. Докажите, что эти точки диаметрально противоположные.
23. В окружности проведены две равные хорды. Докажите, что их концы лежат на параллельных прямых.
24. Чертежным угольником можно рисовать прямые углы. Как с его помощью построить центр данной окружности?

25. Трапеция с углом 20° при основании вписана в окружность, а ее меньшее основание равно боковой стороне. Найдите радиус окружности, если большее основание трапеции равно 1.
26. Трапеция с основаниями а и Ъ вписана в окружность, а ее боковая сторона видна из центра окружности под углом 120°. Найдите диагонали трапеции.
27. Докажите, что серединный перпендикуляр к стороне треугольника и биссектриса его противоположного угла пересекаются на описанной окружности.
28. (Лемма о трезубце.) Биссектриса треугольника пересекает описанную вокруг него окружность в некоторой точке. Докажите, что данная точка равноудалена от двух вершин треугольника и центра вписанной в него окружности.
29. Дан неравнобедренный треугольник. Верно ли, что в нем биссектриса всегда лежит между медианой и высотой, проведенными из одной вершины?
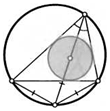
30. В четырехугольник вписана окружность. Четыре меньшие окружности вписаны в углы четырехугольника и касаются первой окружности. Докажите, что отмеченные на чертеже отрезки, соединяющие точки их касания, перпендикулярны.
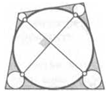
31. В окружность вписан четырехугольник. Оказалось, что он также описан вокруг другой окружности. Докажите, что два отрезка, соединяющих точки ее касания с противоположными сторонами четырехугольника, перпендикулярны.
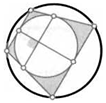
32. Продолжения противоположных сторон АВ и CD вписанного в окружность четырехугольника ABCD пересекаются в точке М, а продолжения сторон ВС и AD — в точке К. Докажите, что биссектрисы углов AMD и CKD перпендикулярны.
33. Две окружности пересекаются в точках А и В. Произвольная прямая пересекает первую окружность в точках М и К, а вторую — в точках Е и F (точка Е лежит на отрезке МК, а точка К — на отрезке EF). Докажите, что /.МАЕ = /КВЕ.
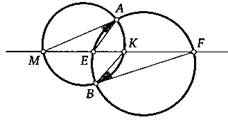
34. В обозначениях предыдущей задачи для случая, когда точка К лежит на отрезке ME, а точка Е — на отрезке KF, докажите, что ZMAE + ZKBF = 180°.
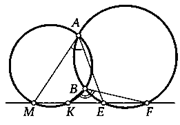
35. На стороне АС треугольника АВС взяли точку М. Пусть Ог и 02 — центры описанных окружностей треугольников АВМ и СВМ. Оказалось, что точки В, М, Ог и 02 лежат на одной окружности. Докажите, что она проходит через середину стороны АС.
36. Докажите, что точки, симметричные ортоцентру треугольника относительно его сторон, лежат на его описанной окружности.