Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Геометрические места точек
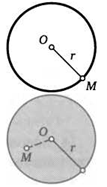
Геометрическим местом точек (ГМТ) называется фигура, состоящая из всех точек плоскости, которые удовлетворяют какому-либо определенному условию.
Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки. Данная точка называется центром окружности, указанное расстояние — ее радиусом.
Круг. — это множество всех точек плоскости, удаленных от данной точки не более, чем на длину данного отрезка. Указанная точка называется центром, а данный отрезок—радиусом круга.
1. (Теорема.) Докажите, что геометрическим местом точек, равноудаленных от двух данных точек Л и Б, является серединный перпендикуляр к отрезку АВ.![]()
2. Даны отрезок АВ и прямая. В каком случае на прямой а) существуют две точки, равноудаленные от Л и Б? б) таких точек нет?
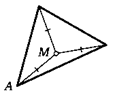
3. Дан треугольник АВС. Где на плоскости находится такая точка М, что AM = ВМ = СМ?
4. Дан четырехугольник ABCD. Где находится такая точка О, что АО = СО, ВО = DO? Сколько может быть таких точек?
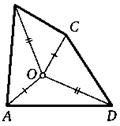
5. Дан четырехугольник ABCD. Оказалось, что на плоскости существуют две такие точки О, что АО = DO, ВО = СО. Докажите, что стороны ВС и AD параллельны.
6. Дан треугольник АВС. Некоторая точка М такова, что AM = 1, ВЫ = 2, СМ = 3. Докажите, что такая точка единственна.
7. На рисунке даны два равных отрезка АВ и CD. Найдите все такие точки М на плоскости, что треугольники АВМ и CDM равны. Сколько существует таких точек?
D О I о Со
8. Дана точка О. Нарисуйте на плоскости множество всех таких точек М, что а) ОМ = 3 см; б) ОМ < 3 см; в) 2 см < ОМ < 3 см.
9. Дан квадрат. Закрасьте внутри него множество всех таких точек М, расстояния от которых до четырех вершин квадрата не больше его стороны.

10. Дан отрезок АВ. Закрасьте на плоскости множество всех таких точек М, что AM < АВ < ВЫ.
11. (Теорема.) Дан отрезок АВ. Докажите, что геометрическим местом таких точек М, что AM < ВЫ, является полуплоскость, расположенная по ту же сторону от серединного перпендикуляра к отрезку АВ, что и точка А.
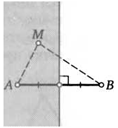
12. Дан отрезок АВ. Где расположены на плоскости все такие точки М, что AM — наименьшая сторона треугольника АМВ? Ответ представьте в виде заштрихованной области.
13. В равностороннем треугольнике АВС взята точка О так, что угол АВО больше 30°. Докажите, что АО > СО.
14. Дан равносторонний треугольник АВС. Изобразите множество всех таких точек М внутри него, что ВЫ меньше AM и СМ.
15. Точка О — середина отрезка МК. Известно, что AM < ВМ, АК < ВК. Докажите, что АО < ВО.
16. Дан квадрат ABCD. Где находятся все такие точки М, что AM<bm<cm<dm7< p=""></bm<cm<dm7<>
*17. Диагонали четырехугольника равны. Известно, что серединный перпендикуляр к одной его стороне пересекает противоположную сторону. Докажите, что это верно и для противоположной стороны.
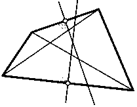
18. (Теорема.) Дан угол меньше развернутого. Докажите, что геометрическим местом точек внутри угла, равноудаленных от его сторон, является биссектриса данного угла.
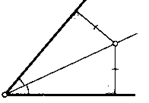
19. Даны две пересекающиеся прямые. Где расположены на плоскости все точки, равноудаленные от этих прямых?
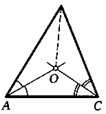
20. Биссектрисы углов Л и С треугольника АВС пересекаются в точке О. Докажите, что эта точка принадлежит и биссектрисе угла В.
В
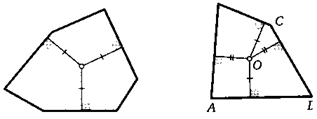
21. Дан шестиугольник, никакие стороны которого не параллельны. Сколько существует точек, которые равноудалены от трех его данных несмежных сторон?
В
D
К задаче 21
К задаче 22
22. Дан выпуклый четырехугольник, у которого нет параллельных сторон. Где находится такая точка, которая одновременно равноудалена от двух пар его противоположных сторон? Сколько может быть таких точек?
23. В четырехугольнике ABCD внешний угол при вершине А равен углу BCD, AD = CD. Докажите, что BD — биссектриса угла
АВС.
В
С
D