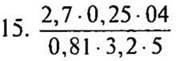Дробные выражения - УМНОЖЕНИЕ И ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ - ОБЫКНОВЕННЫЕ ДРОБИ

Цели: ввести понятия дробного выражения, знаменателя и числителя дробного выражения; формировать устные и письменные вычислительные навыки; повторить теорию по теме «Умножение и деление дробей»; воспитывать умение слушать мнение товарищей.

Ход урока

I. Организационный момент

II. Устная контрольная работа (5 мин)

(На следующем уроке можно поменять варианты.)

Вариант I	Вариант II

III. Сообщение темы урока

— Сегодня на уроке мы узнаем, какие выражения называют дробными. Будем находить значения таких выражений.

IV. Изучение нового материала

1. Подготовительная работа.

— Запишите в виде частного: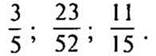

— Запишите в виде дроби: 3 : 7; 43 : 54; 12 : 17.

2. Работа над новой темой.

— Выражение (2,7 + 5,2) : (4,3 — 3,2) можно записать в следующем виде:

— Найдите значение этого выражения. (7.)

Определение. Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.

Например: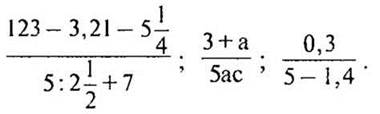

— Приведите примеры дробных выражений. (Запишите на доске несколько примеров.)

Определение. Выражение, стоящее над чертой, называют числителем, а выражение, стоящее под чертой, — знаменателем дробного выражения.

— Назовите числитель и знаменатель данных выражений.

— Сделайте вывод, что может быть числителем и знаменателем дробного выражения. (Любые числа, числовые и буквенные выражения.)

— С дробными выражениями можно выполнять те же действия, что и с обыкновенными дробями.

V. Закрепление изученного материала

Каждое задание выполняют по три ученика у доски, а остальные — в тетрадях, самопроверка.

1. № 693 стр. 111. (Ответ: )

2. № 694 стр. 111.

— Вспомните правила умножения и деления десятичных дробей.

Решение:

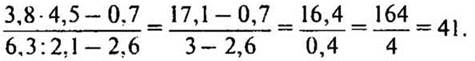
(Все подсчеты в столбик выполняются в тетради.)

3. № 695 (а, г, ж) стр. 111.

— Сформулируйте правило деления смешанных чисел.

— Что называют сокращением дробей?

Решение:

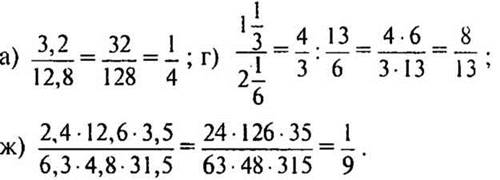
VI. Физкультминутка

VII. Работа над задачей

№ 713 стр. 114 (один ученик решает на обратной стороне доски, остальные в тетрадях, самопроверка).

Решение:

1) 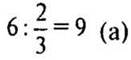— площадь сада.

2) 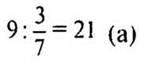- площадь участка.

(Ответ: 21а.)

VIII. Повторение изученного материала

1. Блиц-опрос по теории.

— Расскажите, как умножить дробь на натуральное число.

— Как выполнить умножение двух дробей?

— Как выполнить умножение смешанных чисел?

— Запишите свойства нуля и единицы при умножении.

— Сформулируйте правило деления дробей.

— Как выполняется деление смешанных чисел?

— Сформулируйте правило нахождения дроби от числа.

— Сформулируйте правило нахождения числа по данному значению его дроби.

— Какие числа называют взаимно обратными?

2. Тестовые задания (5 мин. можно выставить оценку).

— Выполните тест.

Вариант I

1. В школе 85 учеников приняли участие в олимпиаде, что составляет 1/10 всех учеников. Сколько учеников в школе?

850 - Ь; 750 - Щ; 520 - X.

2. Найти 40% от 90.

300 - А; 36 - Р; 360 - К

3. В парке 120 деревьев, 5/6 из них березы. Сколько берез в парке?

15 - М; 18 - Л; 100 - Б.

4. Турист прошел 50% пути, что составляет 16 км. Каков путь туриста?

320 - Г; 8 - У; 32 - Д.

5. В хоре 90 человек, 1/10 из них - мальчики. Сколько мальчиков в хоре?

150 - X; 54 - O; 42 - Э.

Запишите ответы в порядке возрастания и прочтите слово.

Ответы:

32	36	54	100	850
Д	Р	О	Б	Ь

Вариант II

1. В ремонте школы приняли участие 94 ученика, что составляет 1/10 всех учащихся школы. Сколько учеников в школе?

940 - Ч; 360 - Л; 54 - М.

2. Найти 20% от 80.

160 - Ц; 16 - О; 200 - В.

3. В саду 50 деревьев, 3/5 яблони. Сколько яблонь растут в саду?

100 - Ч; 250 - Д; 30 - С.

4. Пешеход прошел 8 км, что составляет 40% всего пути. Каков путь пешехода?

30 - Ж; 16 - Э; 20 - Л.

5. В хоре 30 девочек, что составляет 2/5 всех учащихся в хоре. Сколько всего учащихся в хоре?

12 - К; 125 - Ж; 75 - И.

Запишите ответы в порядке убывания и прочтите слово.

Ответы:

940	75	30	20	16
Ч	И	С	Л	О

IX. Подведение итогов урока

— Как называются выражения, находящиеся над чертой? Под чертой?

— Каким может быть числитель и знаменатель дробного выражения?

Домашнее задание

№ 710 , 716 (а, е) стр. 114; № 705 стр. 113.