Поурочные разработки по Математике 6 класс
Раскрытие скобок - урок 2 - РЕШЕНИЕ УРАВНЕНИЙ - РАЦИОНАЛЬНЫЕ ЧИСЛА
Цели: отрабатывать умение раскрывать скобки при упрощении выражений, решении уравнений и задач, решать уравнения несколькими способами; развивать грамотную математическую речь, память, внимание.
Ход урока
I. Организационный момент
II. Устный счет
1. Раскройте скобки:

2. Выполните действия:
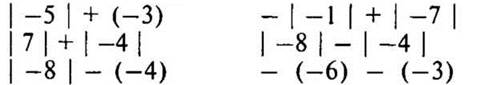
3. Решите уравнения:
![]()
III. Индивидуальная работа
1 карточка
Выполните деление:

2 карточка
Выполните деление:
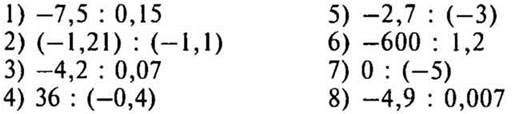
IV. Сообщение темы урока
— Сегодня мы продолжим раскрывать скобки при упрощении выражений, решении уравнений и задач.
V. Закрепление изученного материала
1. « 1238 (2 столбик) стр. 217 (самостоятельно, взаимопроверка).
(Ответ:
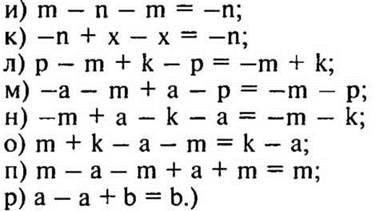
3. № 1241 (в, г) стр. 217 (на обратной стороне доски, самопроверка).
— На чем основаны разные способы решения уравнений?
в) 1 способ

2 способ
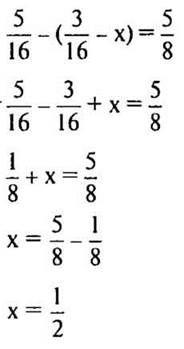
г) 1 способ
(х + 3) - 17 = -20
х + 3 = -20 + 17
х + 3 = -3
х = -3 - 3
х = -6
2 способ
(х + 3) - 17 = -20
х + 3 - 17 = -20
х - 14 = -20
х = -20 + 14
х = -6
(Ответ: в) х = 1/2; г) x = -6.)
VI. Самостоятельная работа
Вариант I
1. Раскройте скобки и найдите значение выражения:
а) 8,3 + (4,5 - 6,3); б) 4,1 - (5,6 - 6,9).
2. Составьте сумму выражений m + 4,8 и —3,2 - m и упростите ее.
3. Составьте разность выражений 24 — у и —12 — у и упростите ее.
4. Решите уравнение:
а) 8,4 - (х - 36) = 18; б) 9,3 + (3,1 - у) = 12,2.
Вариант II
1. Раскройте скобки и найдите значение выражения:
а) 5,94 + (7,2 - 4,14); б) 8,31 - (7,2 - 1,89).
2. Составьте сумму выражений х + 12 и —16 — х и упростите ее.
3. Составьте разность выражений 4,8 + n и —6,3 + n и упростите ее.
4. Решите уравнение:
а) 9,6 - (2,6 - у) = 4; б) -4,2 + (х - 5,8) = 2,5.
VII. Физкультминутка
VIII. Работа над задачей
1. № 1242 (а) стр. 218 (у доски и в тетрадях с подробным комментированием).
— Прочитайте задачу.
— Составьте краткую запись в виде таблицы.
— Что известно? Что надо узнать?
Было |
Сняли |
Осталось |
|
1 полка 2 полка |
42 кн. 34 кн. |
? кн,столько, сколько ост. на 2 полке ? кн. |
12 кн. ? кн. |
Пусть х (кн.) — сняли со 2 полки.
Было |
Сняли |
Осталось |
|
1 полка 2 полка |
42 кн. 34 кн. |
(34 — х) кн. х кн. |
42 — (34 — х) кн. (34 — х) кн. |
Зная, что на 1 полке осталось 12 книг после того, как сняли книги, составим уравнение:
42 - (34 - х) = 12
42 - 34 + х = 12
8 + х = 12
х = 4; 4 кн. — сняли со 2 полки.
(Ответ: 4 книги.)
2. № 1249 стр. 219 (у доски и в тетрадях с подробным комментированием).
— Прочитайте задачу.
— Что такое граф? (Геометрические фигуры, состоящие из точек (которые называют вершинами) и соединяющих их отрезков (называемых ребрами графа).)
— О ком идет речь в задаче?
— Что о них известно?
Решение:
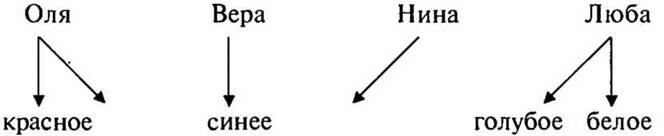
Предположим, что в пункте 1) утверждение «Оля — в синем» верно, тогда в пункте 2) утверждение «Оля — в красном» — неверно и должно быть верным утверждение «Нина — в синем», но это будет противоречить нашему предположению из пункта 1) что «Оля — в синем» — верно, значит, в пункте 1) верным является утверждение «Люба — в белом». Из пункта 3) следует, что утверждение «Вера - в синем» - верно, а из пункта 2) следует, что верно утверждение «Оля — в красном». Для Нины остается один вариант: «Нина — в голубом».
(Ответ: Люба — в белом, Вера - в синем, Оля — в красном, Нина — в голубом.)
IX. Повторение изученного материала
1. Определите порядок действий и запишите программу их выполнения:
а3 + b · (с — d2) + (е · f — к).
2. № 1246 (а, б) стр. 218 (с объяснением у доски и в тетрадях).
— Какие числа называются целыми? (Натуральные числа, противоположные им числа и нуль называют целыми числами.)
(Ответ: а) -12; -11; -10; -9; б) -21; -20; -19; -18.)
3. № 1253 (а) стр. 219 (у доски и в тетрадях).
— На чем основано решение уравнения? (Распределительное свойство умножения.)
Решение:
-2(3,1х - 1) + 3(1,2х + 1) = -14,5
-6,2х + 2 + 3,6х + 3 = -14,5
-2,6х + 5 = -14,5
-2,6х = -14,5 - 5
-2,6х = -19,5
х = -19,5 : (-2,6)
х = 7,5
(Ответ: х = 7,5.)
X. Подведение итогов урока
— Для чего в выражениях раскрывают скобки? (Для упрощения вычислений.)
— Чему равна сумма противоположных чисел?
Домашнее задание
№ 1254 (в, г) стр. 219; № 1255 (в, г), 1256 (в, г), 1258 (б);№ 1259(6) стр. 220.