ДЕЛЕНИЕ - урок 5

«Я люблю математику не только потому, что

она находит применение в технике, но и потому,

что она красива».

Петер Ропсе

Оборудование: тексты задач на плакатах; ксерокопии листов с домашним заданием; плакаты с высказываниями о задачах; костюм для дяди Степы-милиционера.

«Математическая задача иногда столь же увлекательна, как кроссворд, и напряженная умственная работа может быть столь же желанным упражнением, как стремительный теннис».

Д. Пойа

«Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдется путь!»

Д. Пойа

«При решении задачи плохой план часто оказывается полезным, он может вести к лучшему плану».

Д. Пойа

«В задачах, которые ставит перед нами жизнь экзаменатором является сама природа».

У. Сойер

Ход урока

I. Устные упражнения.

На доске записаны краткие условия задач.

1. Из пунктов А и В навстречу друг другу выехали автомобиль со скоростью 60 км/ч и велосипедист со скоростью 15 км/ч. Встретятся ли автомобиль и велосипедист через 2 часа, если расстояние между пунктами 160 км? (Решить задачу двумя способами.)

2. Из лагеря геологоразведчиков выехал вездеход со скоростью 30 км/ч. Через 2 часа вслед за ним был послан другой вездеход. С какой скоростью он должен ехать, чтобы догнать первый через 4 часа после своего выхода? (Можно сделать чертеж к задаче.)

II. Работа по теме урока.

1. Повторить, как найти расстояние, время, скорость, и решить задачи.

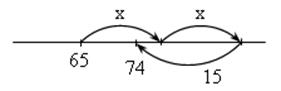
2. По рисунку составить задачу на движение и решить ее.

3. Викторина (3 ученика).

а) Первый ученик: «Автомобиль «Москвич» за 3 часа может проехать 360 км. Бескрылая птица страус – лучший бегун в мире – развивает скорость до 120 км/ч. Сравните скорости автомобиля «Москвич» и страуса».

б) Второй ученик предлагает классу свою задачу.

«Скорость распространения света самая большая в природе – 300000 км/с. На Солнце произошла вспышка. Через какое время ее увидят на Земле, если расстояние от Земли до Солнца равно 150000000 км?

в) Третий ученик:

«Пройденный путь пешехода S, его скорость  и время движения t связаны соотношением S = t. Если пешеход за 4 часа прошел 24 км, то его скорость равна:

1) 12 км/ч; 2) 6 км/ч; 3) 96 км/ч; 4) 8 км/ч.

4. Решить олимпиадную задачу.

Из пунктов А и В, расстояние между которыми 100 км, со скоростями 20 км/ч и 30 км/ч выезжают навстречу друг другу два велосипедиста. Вместе с ними со скоростью 50 км/ч вылетают две мухи, летят до встречи, поворачивают и летят обратно до встречи с велосипедистами, снова поворачивают и т. д. Сколько километров пролетит каждая муха в направлении от А до В до того момента, когда велосипедисты встретятся?

Решение: Велосипедисты встретятся через 2 часа на расстоянии 40 км/ч от А. За это время каждая муха пролетела 100 км. Муха, вылетевшая из А, пролетела в направлении от А до В на 40 км больше, чем в обратном направлении, и поэтому от АВ она пролетела 70 км. Аналогично, вторая муха в направлении от А к В пролетела на 60 км меньше, чем в обратном, то есть 20 км.

Ответ: первая муха в направлении от А к В пролетела 70 км, вторая – 20 км.

5. Входит дядя Степа-милиционер и предлагает задачу из сборника задач по основам безопасности дорожного движения.

а) Ширина проезжей части дороги 15 м, зеленый сигнал светофора горит 20 секунд. С какой наименьшей скоростью может двигаться пешеход с момента загорания светофора, чтобы благополучно перейти дорогу?

Решение:

1) 15 м = 1500 см

2) 1500 : 20 = 75 см/с.

Ответ: пешеход может двигаться со скоростью 75 см/с.

б) Мотоциклист едет со скоростью 95 км/ч, а скорость велосипедиста на 76 км/ч меньше. Во сколько раз скорость мотоциклиста больше скорости велосипедиста? Кому из них легче остановиться?

Решение:

1) 95 – 76 = 19 км/ч

2) 95 : 19 = 5 раз.

Ответ: в 5 раз легче остановиться велосипедисту, так как при меньшей скорости короче тормозной путь.

III. Итог урока.

Отметить особо отличившихся учеников, если есть возможность, то наградить сувенирами.

VI. Домашнее задание: ученикам раздаются ксерокопии заданий.

1) Помогите французским девочкам.

Однажды Жанин и Моника поплыли по маленькой речке, отправившись из одного и того же места, но только Жанин поплыла против течения, а Моника поплыла по течению. Оказалось, что Моника забыла снять большие деревянные бусы. Через четверть часа девочки повернули обратно. Кто же из них подберет бусы Моники: сама Моника или Жанин? (Скорость обеих пловчих в неподвижной воде одинакова.)

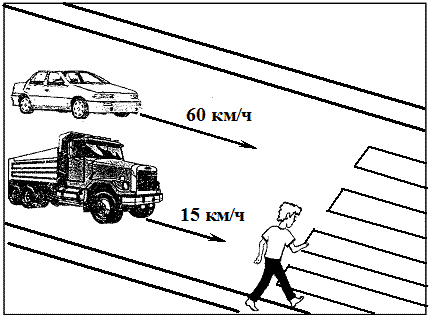
2) Задача от дяди Степы.

Скорость легкового автомобиля 60 км/ч, а грузовика 15 км/ч. Во сколько раз скорость легкового автомобиля больше скорости грузовика? Какой автомобиль опаснее для школьника, начавшего движение по пешеходному переходу?

3) Задание от «Знающего человека». Заполнить таблицу.

Объект	Скорость 	Время t	Расстояние S
«Волга»	100 км/ч	5 ч
«Ока»	60 км/ч		420 км
«Москвич»		3 ч	240 км
Пчела	60 км/ч		180 км
Стрекоза		2 ч	200 км
Стриж	100 км/ч	4 ч
Меч-рыба	100 км/ч		300 км
Земля (вокруг Солнца)	30 км/ч	24 ч
Черепаха		6 мин	18 м
Улитка		7 ч	35 км
Верблюд	8 км/ч	5 ч
Почтовый голубь	50 км/ч		150 км

4) Составить по одной анаграмме.

Ответы для учителя.

Задача № 1

Скорости девушек относительно неподвижной воды одинакова. Но ведь по отношению к воде в реке бусы остаются неподвижными – они движутся в точности с такой же скоростью, что и вода (со скоростью течения). Пловчихи проплывают относительно воды одинаковое расстояние и по истечении получаса встречаются в том месте, где в этот момент находятся бусы. Таким образом, обе девушки могут подобрать бусы с равным основанием, так как встречаются в тот самый момент, когда подплывут бусы.

Задача № 2

Опаснее легковой автомобиль, так как у него скорость больше, кроме того, для водителя легкового автомобиля мальчик появится неожиданно, так как обзор будет закрыт грузовым автомобилем.