Перебор возможных вариантов - Перебор возможных вариантов - Натуральные числа

Цель: сформировать первоначальные навыки решения комбинаторных задач с помощью перебора возможных вариантов.

I . Организационный момент.

II. Устная работа.

Заполните пустые ячейки таким образом, чтобы сумма в вертикальных, горизонтальных и диагональных рядах была равна 27, при этом ни одно число в каждом примере не должно повториться.

III. Актуализация знаний.

Организовать работу в группах по решению задач с последующим обсуждением.

Группа 1. В воскресенье трое друзей (Миша, Саша и Дима) решили пойти в парк. Они пришли к аттракциону «Автодром». По правилам в одну машину садятся двое: водитель и пассажир. Чтобы никому не было обидно, ребята решили: каждый должен побывать водителем и каждый должен покататься одинаковое число раз. Какое решение они нашли?

Ответ: составляются следующие пары: Миша — Саша, Саша — Дима, Дима — Миша (имя водителя подчеркнуто). В данной задаче есть возможность прийти к решению, разыгрывая сценку с детьми.

Группа 2. Учительница сказала, что Аня, Катя и Даша написали контрольную работу на отметки «4» и «5», но, кто из них какую отметку получил, не назвала. Какие отметки могут быть у девочек?

Решению задачи может помочь таблица:

Аня	5	5	5	4	4	4	5	4
Катя	5	4	5	5	5	4	4	4
Даша	5	5	4	5	4	5	4	4

Группа 3. Для волейбольной команды вымпел сшивается из двух треугольных кусочков ткани разного цвета. Имеется ткань четырех цветов: желтого, зеленого, красного и синего. Сколько разных вымпелов можно изготовить?

В ходе решения задачи можно организовать практическую деятельность по изготовлению вымпелов из цветной бумаги. Ответ: жз, жк, же, зк, зс, кс.

Группа 4. Ученик нарисовал в ряд четыре фигуры — большой и маленький квадраты, большой и маленький круги — и расположил их так, что на первом месте находится круг и одинаковые по форме фигуры не стоят рядом. В какой последовательности расположены эти фигуры?

Учащиеся с помощью заготовленных фигур демонстрируют все возможные варианты (рис. 35).

Ответ:

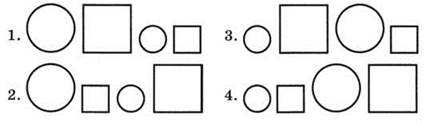
Рис. 35

IV. Изучение нового материала.

1. Объяснение учителя.

В повседневной жизни нередко у нас возникают проблемы, которые имеют не одно, а несколько различных вариантов решения. Чтобы сделать правильный выбор, очень важно не упустить ни один из них. Для этого надо осуществить перебор всех возможных вариантов или хотя бы подсчитать их число. Такого рода задачи называются комбинаторными. Решить задачу — это значит ответить на вопрос, сколько существует возможных вариантов, и выписать все возможные комбинации, составленные из чисел, слов, предметов и т. д., отвечающих условию. При решении каждой задачи ставится один и тот же вопрос: как организовать перебор вариантов, чтобы не пропустить ни один из них и в то же время избежать повтора?

2. Решение и обсуждение задач.

1). РТ, часть 2, № 3.

Выписать все варианты:

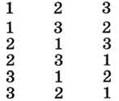
Обратить внимание учащихся на запись и закономерность.

2). Разобрать пример 3 из учебника. Обратить внимание учащихся на логику перебора и на то, что АВ и ВА — это один и тот же вариант.

3). У, № 157. Обратить внимание учащихся на то, что двузначное число не может начинаться с цифры О. Далее возможны два варианта решения задачи. Можно сразу выписать числа 10, 12, 20, 21, отбросив в уме не устраивающие нас числа 11 и 22. А можно записать все возможные двузначные числа, состоящие из данных цифр в порядке возрастания: 10, 11, 12, 20, 21, 22 — и вычеркнуть числа 11, 22, состоящие из одинаковых цифр.

4). У, № 161, 162. Задачи выполняются по вариантам. Условия задач разные, модель одна — составление трехзначного числа, в котором все цифры разные.

5). У, № 163 (а). Идея кодирования: Р — русский язык, М — математика, Ф — физкультура.

Р М .

Р Ф .

М Р .

М Ф .

Ф М .

Ф Р М

Ответ: 6 вариантов.

6). У, № 164 (а). Обратить внимание учащихся на то, что: 1) ШЛ и ЛШ — один и тот же вариант; 2) всего имеется 4 игры, варианты ШШ, КК, ЛЛ, ЭЭ невозможны.

ШЛ, ШК, ШЭ

ЛК, Л.

КЭ

Ответ: 6 вариантов.

V. Итоги урока.

1. Какие задачи называются комбинаторными?

2. Что значит решить комбинаторную задачу?

VI. Домашнее задание.

У, п. 2.5, № 156, 158, 163 (б), 164 (б).