Знакочередующиеся ряды - РЯДЫ

Числовой ряд называется знакочередующимся, если любые два рядом стоящих члена его имеют противоположные знаки.

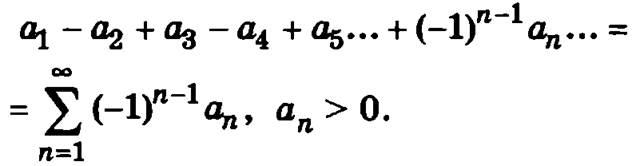
Признак сходимости знакочередующегося ряда (признак Лейбница)

Если члены знакочередующегося ряда убывают по абсолютной величине a1 ≤ a2 ≤ a3 ≤ а4 ≤ a5... и предел то ряд будет сходиться и его сумма S не превзойдетa1.

Пример. Рассмотрим знакочередующийся ряд

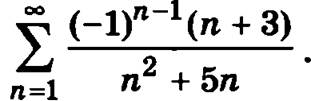
Докажем, что члены знакочередующегося ряда убывают по абсолютной величине, то есть что аn ≥ аn+1. В данном случае 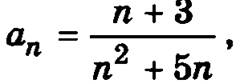а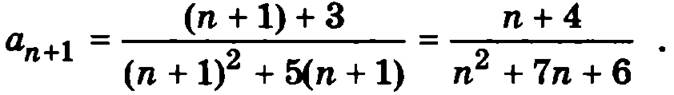

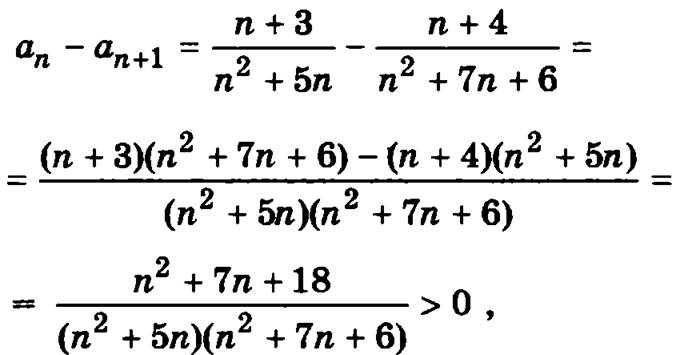
следовательно, аn – аn-1 > 0 и аn > аn+1.

Вычислим предел

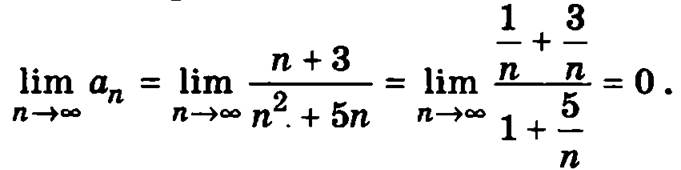
Таким образом, оба условия признака Лейбница выполнены и исследуемый ряд сходится.