Высшая математика мини-справочник для ВУЗов
Линейные дифференциальные уравнения первого порядка - ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Линейными уравнениями первого порядка называются уравнения вида
у' + р(х)у = q(x),
где р(х), q(x) — заданные функции.
Будем искать решение линейного уравнения в виде произведения двух неизвестных функций u(х) и v(x):
у = u(x)v(x).
Подставим указанный вид решения в уравнение
u'v + uv' + p(x)uv = р(х).
Сгруппируем второе и третье слагаемые в левой части и вынесем за скобки их общий множитель u:
u'v + u(v' + p(x)v) = р(х).
Выберем функцию v(х) таким образом, чтобы обратилось в ноль выражение в скобках:
v' + р(x)v = 0.
Данное соотношение можно рассматривать как дифференциальное уравнение с разделяющимися переменными относительно неизвестной функции v(x), которое представим в виде
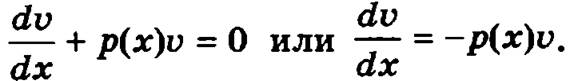
Умножим полученное уравнение на dx, а затем разделим на v:
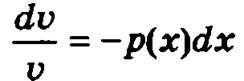
и проинтегрируем:
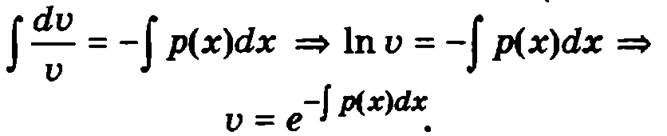
Обращаем внимание на то, что в данном случае отсутствует произвольная постоянная с, которая появляется при вычислении неопределенного интеграла и которая всегда присутствовала в ранее рассмотренных случаях. Это объясняется тем, что для построения решения подойдет любая функция v, обращающая в ноль выражение в скобках v' + р(х)v = 0, в том числе и та, которая соответствует с = 0.
Учитывая вышеизложенное, для определения функции и получим следующее дифференциальное уравнение, которое тоже будет уравнением с разделяющимися переменными u'v = р(х) или с учетом определенного ранее вида функции 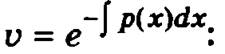
![]()
Заменим производную u' отношением дифференциалов:
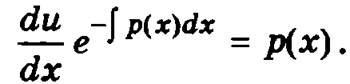
Умножим обе части полученного уравнения на ![]()
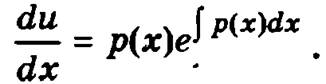
Интегрированием найдем выражение для функции u:
![]()
Тогда окончательное общее решение исходного дифференциального уравнения будет иметь вид
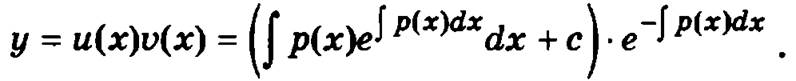
Пример. Найти частное решение дифференциального уравнения ![]() удовлетворяющее начальному условию у(1) = 0.
удовлетворяющее начальному условию у(1) = 0.
Реализуя метод решения линейных дифференциальных уравнений первого порядка, будем искать решение в виде у = u ∙ v. Тогда у = u'v + uv' и исходное уравнение примет вид
![]()
Далее, следуя соответствующему алгоритму, получим:
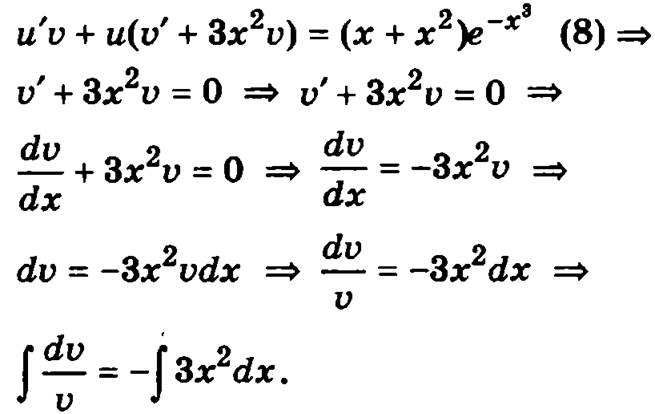
Интеграл 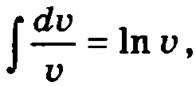 а интеграл
а интеграл 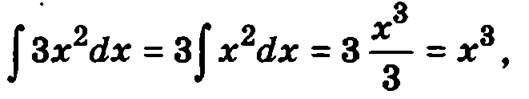 тогда
тогда ![]()
Подставляя полученное значение v в (8) и учитывая, что при этом v' + 3x2v = 0, будем иметь ![]() или u' = (х + x2).
или u' = (х + x2).
Следовательно
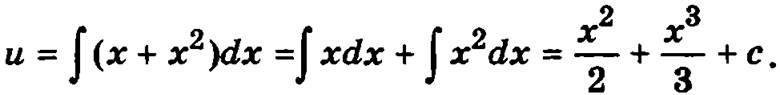
Перемножая полученные выражения для функций u и v, найдем общее решение исходного дифференциального уравнения:
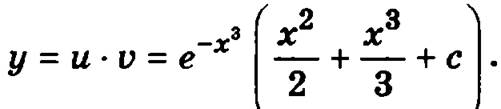
Для определения постоянной с вычислим значение полученного выражения для общего решения уравнения при х = 1 и потребуем, чтобы оно равнялось 0, как того требует поставленное начальное условие:
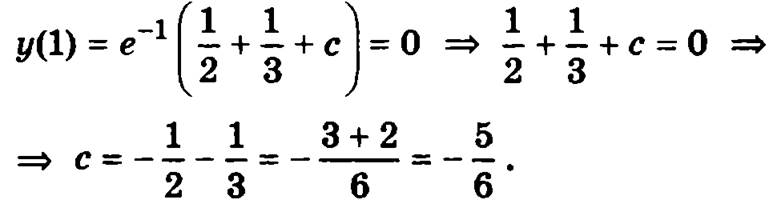
Подставив найденное значение с в общее решение исходного дифференциального уравнения, получим частное решение этого же уравнения, удовлетворяющее указанному начальному условию: