Дифференциальные уравнения с разделяющимися переменными - ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Дифференциальными уравнениями с разделяющимися переменными называются дифференциальные уравнения первого порядка вида

Заменим в уравнении производную неизвестной функции у отношением дифференциалов неизвестной функции dy и независимой переменной dx, получим

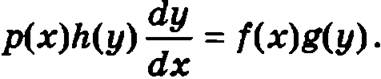
Теперь для разделения переменных разнесем дифференциалы переменных dx и dy по разные стороны знака равенства, для чего умножим обе части уравнения на dx:

Завершая процесс разделения переменных, перенесем функцию р(х) влево, a g(y) — вправо, разделив обе части уравнения на р(х) ∙ g(y):

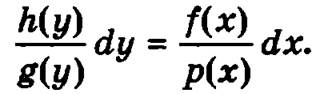
Интегрируя это равенство, получим общее решение исходного уравнения:

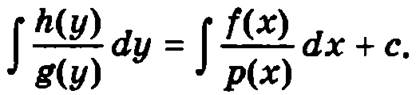
Пример. Найти частное решение дифференциального уравнения 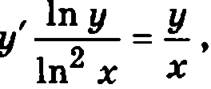удовлетворяющее начальному условию у(1) = 1.

Заменив производную в уравнении отношением дифференциалов dy/dx,

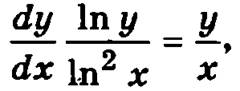
умножим обе части уравнения на dx

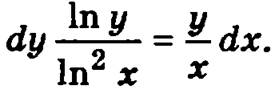
Далее разделим обе части полученного соотношения на y/ln2 x

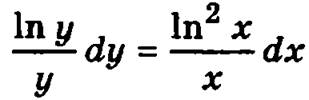
и проинтегрируем его

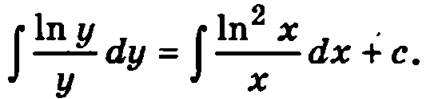
Для вычисления интеграла 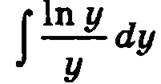введем новую переменную интегрирования z = ln у, тогда

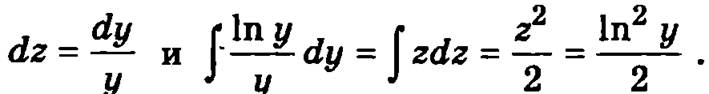
Во втором интеграле 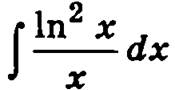сделаем замену переменной интегрирования, положив t = ln x, dt = dx/x. В этом случае получим

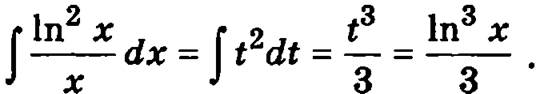
Окончательно общее решение можно представить в виде

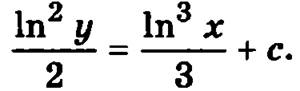
Потребуем выполнения условия y(1) = 1, для чего в полученное общее решение исходного дифференциального уравнения подставим х = 1 и у = 1:

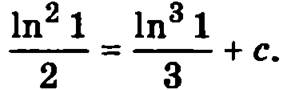
Учитывая, что логарифм единицы равен нулю, для произвольной постоянной получим С = 0. Подставляя найденное значение С в общее решение уравнения, определим окончательный вид частного решения, удовлетворяющее поставленным начальным условиям y(1) = 1:

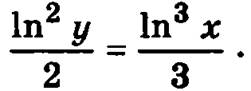
Если существует такое у0, что g(y0) = 0, то постоянная функция у = y0 так же будет решением уравнения, в чем легко убедиться подстановкой этой функции в уравнение:

Левая часть данного уравнения будет равна нулю в силу равенства нулю производной dy0/dx = 0 как величины постоянной, а правая часть уравнения равна нулю в силу того, что g(y0) =0. Это решение нельзя получить из общего решения ни при каких значениях произвольной постоянной. Такие решения дифференциальных уравнений называются особыми.