Высшая математика мини-справочник для ВУЗов
Наибольшее и наименьшее значения функции нескольких переменных - ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Если функция определена и непрерывна в ограниченной замкнутой области Q, то она достигает на этой области своих наибольшего и наименьшего значений. Рассмотрим алгоритм нахождения наибольшего и наименьшего значений функции на конкретном примере.
Найдем наибольшее и наименьшее значения функции ![]() в замкнутой области: х ≥ -1, у ≥ -1, х + у ≤ 1.
в замкнутой области: х ≥ -1, у ≥ -1, х + у ≤ 1.
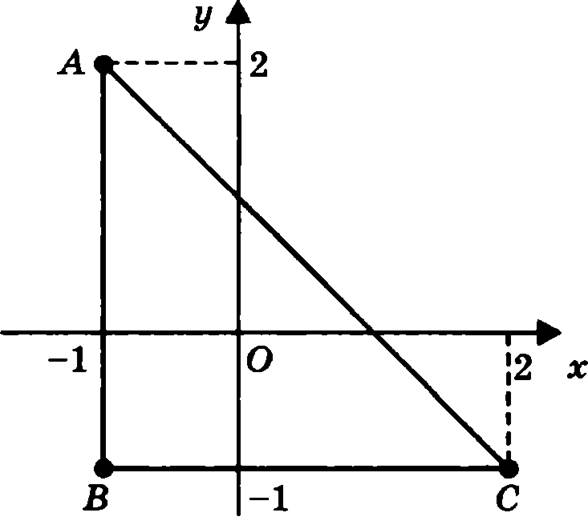
Рис. 10
Определим стационарные точки функции
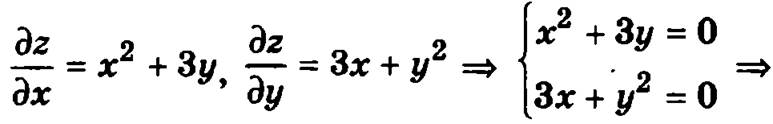
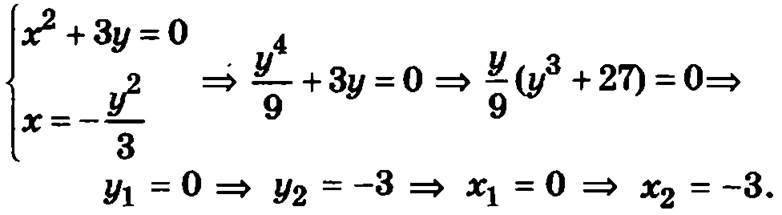
Таким образом, функция имеет две стационарные точки O(0, 0) и М(-3, -3). Если наибольшее или наименьшее значение функция достигает внутри области, то это возможно лишь в стационарных точках, принадлежащих данной области, т.е. в рассматриваемом случае в точке O(0, 0). Поэтому точку М2(-3, -3) исключаем из рассмотрения.
Исследуем теперь границу области, которая состоит из трех участков АВ, ВС и АС. Рассмотрим каждый участок отдельно. Уравнение участка АВ границы х = -1 подставим в исследуемую функцию, получим ![]() где -1 ≤ y ≤ 2. Таким образом, необходимо определить наименьшее и наибольшее значения функции одной переменной
где -1 ≤ y ≤ 2. Таким образом, необходимо определить наименьшее и наибольшее значения функции одной переменной ![]() на отрезке -1 ≤ у ≤ 2.
на отрезке -1 ≤ у ≤ 2.
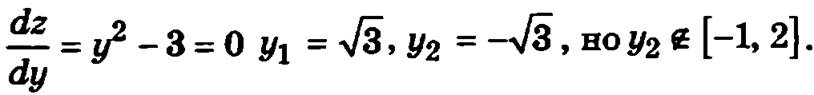
Значит функция может принимать наибольшее и наименьшее значения в точке y1 = √3 и на границе отрезка в точках -1 и 2. Следовательно, к точке О добавим еще и точки В(-1, -1),K(-1, √3) и А(-1, 2).
Уравнение участка ВС у = -1, а рассматриваемая функция на этом участке имеет вид
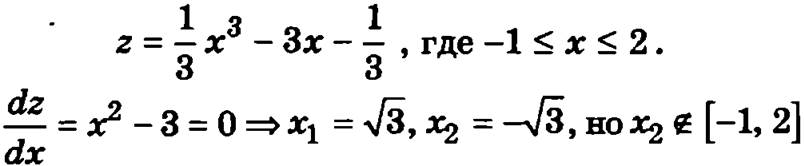
и функция может достигать наибольшее и наименьшее значения в точке x1 = √3 и на границе отрезка в точках -1 и 2. Поэтому к ранее отобранным точкам добавим точки К2(√3, -1) и С(2, -1).
Уравнение участка АС x + у = 1 или у = 1 - х. Подставив уравнение этого участка границы в рассматриваемую функцию, получим
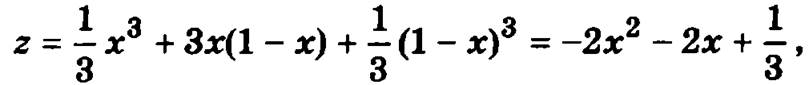
где -1 ≤ х ≤ 2.
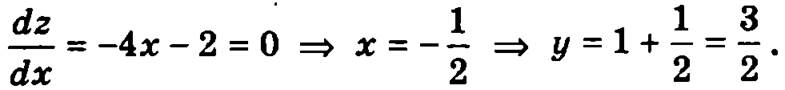
Это дает нам еще одну точку K3(-1/2, 3/2) (точки, соответствующие граничным значениям рассматриваемого отрезка -1 ≤ х ≤ 2 В(-1, -1) и С(2, -1), были отобраны ранее).
Вычислим значения функции 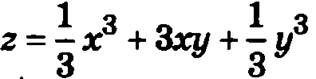 в точках А, В, С, K1, K2 K3, O
в точках А, В, С, K1, K2 K3, O
![]()
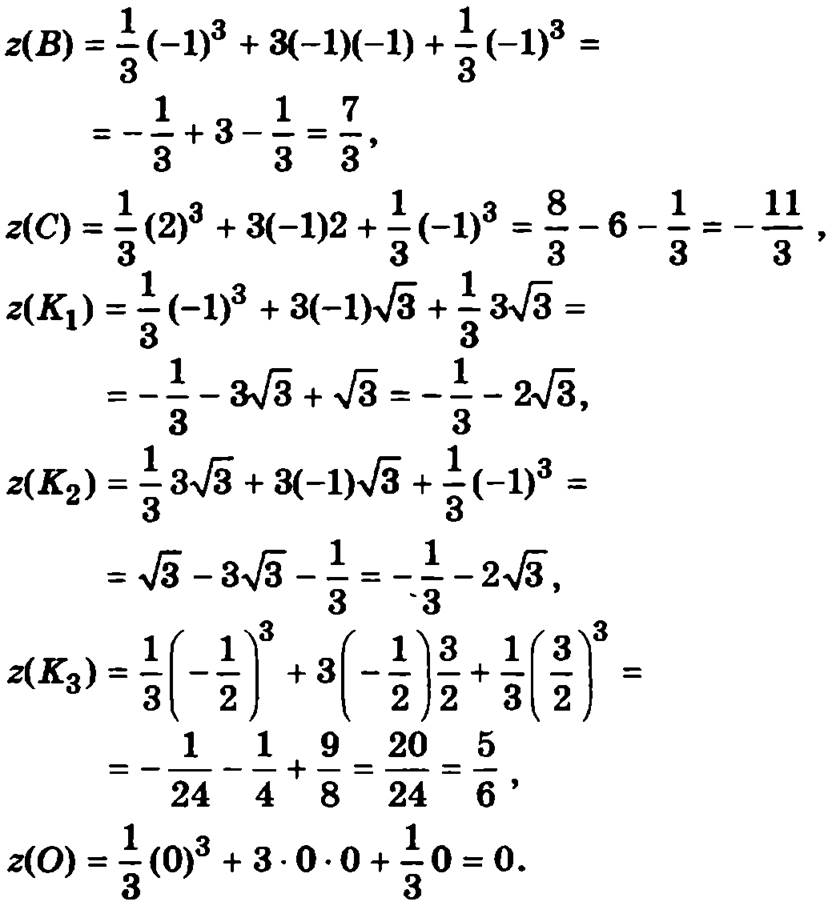
Выбирая из вычисленных значений наибольшее и наименьшее, получим, соответственно, наибольшее и наименьшее значения данной функции на рассматриваемом множестве. Следовательно, наименьшим значением функции будет -1/3 — 2√3, которое достигается в точках К1 и К2, а наибольшим — 7/3, которое достигается в точке В.