Высшая математика мини-справочник для ВУЗов
Исследование функций - ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Исследование функций проводится по следующему плану:
1. Находится область определения функции.
2. Находятся точки пересечения графика функции с осями координат.
3. Определить, является ли функция четной или нечетной.
4. Определяются интервалы возрастания и убывания функции, точки ее экстремумов.
5. Определяются интервалы выпуклости и вогнутости графика функции.
6. Находятся асимптоты графика функции.
7. Строится график функции.
Пример. Исследуем функцию 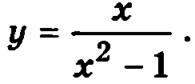
1. Областью определения функции будет вся числовая ось, за исключением тех точек, в которых знаменатель обращается в ноль х2 - 1 = 0, то есть за исключением точек х = -1 и х = 1.
2. Для определения точек пересечения графика функции с осью ОХ следует решить уравнение 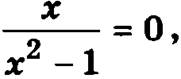 которое имеет единственное решение х = 0. Таким образом, график пересекает ось ОХ в точке х = 0.
которое имеет единственное решение х = 0. Таким образом, график пересекает ось ОХ в точке х = 0.
Положив х = 0, можно найти точку пересечения с осью OY, она совпадет в данном случае с выше найденной точкой.
3. Исследуем функцию на четность. Функция называется четной, если выполняется соотношение у(-х) = у(х), и функция называется нечетной, если для нее справедливо соотношение у(-х) = -у(х).
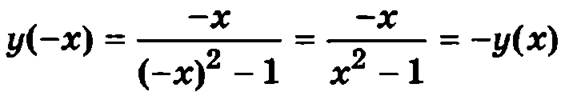
Таким образом, данная функция является нечетной.
4. Для определения интервалов возрастания и убывания найдем производную функции:
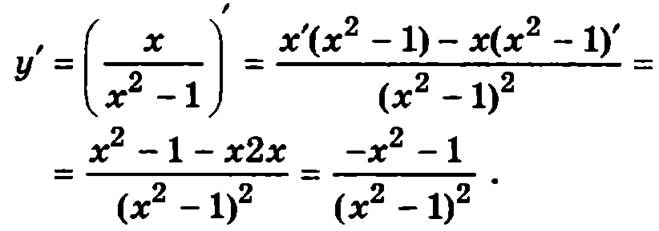
Далее найдем нули числителя и знаменателя полученного выражения:
![]() числитель нулей не имеет,
числитель нулей не имеет,
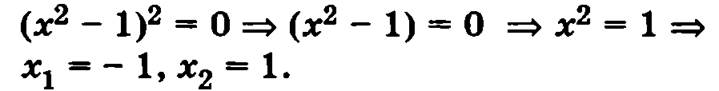
Отмечаем полученные значения на числовой оси:

Числовая ось разделилась на три интервала. Возьмем по одной точке на каждом интервале, например -2, 0 и 2, и вычислим в них значение первой производной:
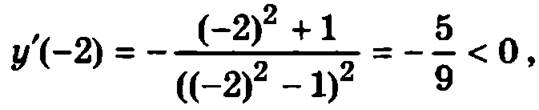
значит производная на всем интервале (-∞, -1), которому принадлежит точка х = -2, будет отрицательной и на этом интервале функция будет убывать;
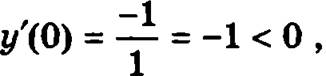 точка х = 0 принадлежит интервалу (-1, 1), и на всем этом интервале производная тоже будет отрицательной, а функция будет убывать;
точка х = 0 принадлежит интервалу (-1, 1), и на всем этом интервале производная тоже будет отрицательной, а функция будет убывать;
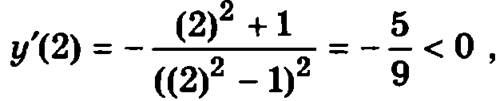 из чего следует, что и на всем интервале (1, +∞) функция будет убывающей.
из чего следует, что и на всем интервале (1, +∞) функция будет убывающей.
На всей области определения производная функции отрицательна, следовательно, на всей области определения функция убывает, и потому экстремумов у нее нет.
5. Найдем вторую производную функции:
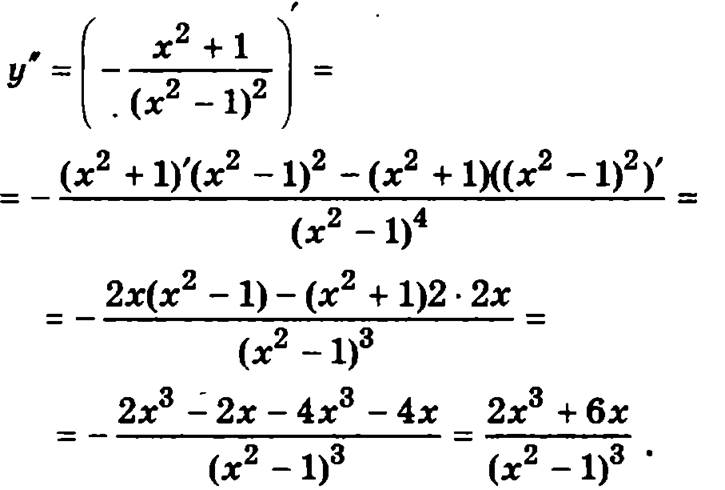
Найдем нули числителя и знаменателя полученной дроби:
![]()
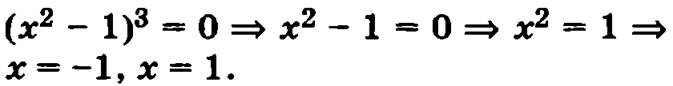
Отметим нули числителя и знаменателя на числовой оси:

Чтобы определить знак второй производной на каждом из полученных интервалов, вычислим ее значение в точках -2; -0,5; 0,5 и 2, принадлежащих этим интервалам:
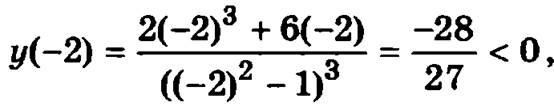 следовательно всюду на интервале (-∞, -1) вторая производная функции отрицательна, а график функции выпуклый;
следовательно всюду на интервале (-∞, -1) вторая производная функции отрицательна, а график функции выпуклый;
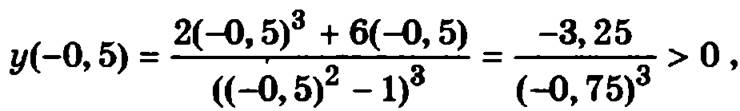 значит вторая производная на интервале (-1, 0), которому принадлежит точка -0,5, положительна, и график функции на этом интервале вогнутый;
значит вторая производная на интервале (-1, 0), которому принадлежит точка -0,5, положительна, и график функции на этом интервале вогнутый;
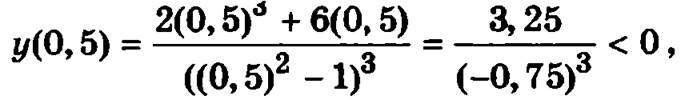 вторая производная на интервале (0, 1), которому принадлежит точка 0,5, отрицательна, и график функции на этом интервале выпуклый;
вторая производная на интервале (0, 1), которому принадлежит точка 0,5, отрицательна, и график функции на этом интервале выпуклый;
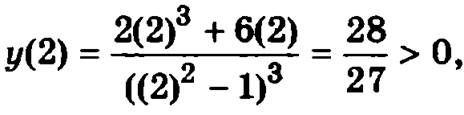 на интервале (1, +∞) вторая производная положительна, а график функции вогнутый.
на интервале (1, +∞) вторая производная положительна, а график функции вогнутый.
Точкой перегиба графика функции-будет точка х = 0, так как она отделяет интервал вогнутости (-1, 0) от интервала выпуклости (0, 1).
6. Найдем односторонние пределы функции в точках x = -1 и х = 1, где она не определена:
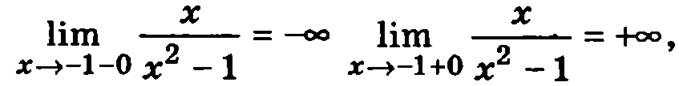 значит в точке х = -1 функция имеет разрыв второго рода;
значит в точке х = -1 функция имеет разрыв второго рода;
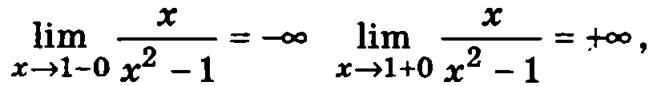 значит в точке х = 1 функция тоже имеет разрыв второго рода.
значит в точке х = 1 функция тоже имеет разрыв второго рода.
Таким образом, график функции имеет две вертикальные асимптоты х = -1 и х = 1.
Для нахождения невертикальных асимптот вычислим пределы:
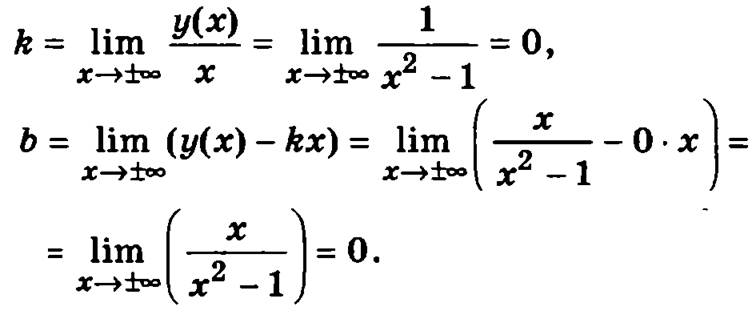
Следовательно, график функции имеет невертикальную асимптоту у = 0.
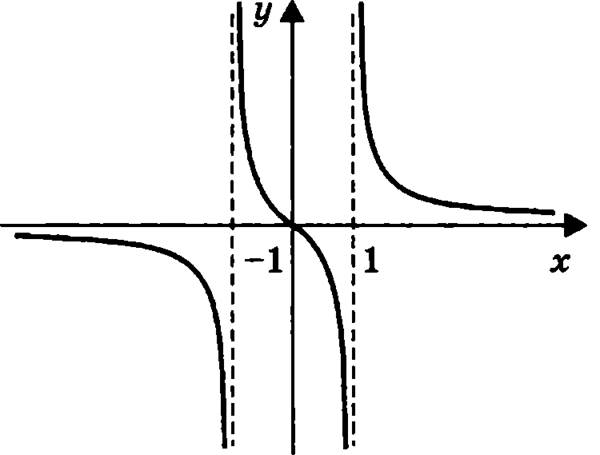
Рис. 9
На рис. 9 изображен график данной функции.