Математика 9 класс подготовка к ГИА
Вариант № 4 - Учебно-тренировочные тесты
Вариант № 4
Часть I
Модуль «Алгебра»
1. Найдите значение выражения ![]()
1) .
2) -1.
3) 1.
4) 30/7
2. На координатной прямой (см. рис. 24) отмечены числа а и b.
![]()
Рис. 24
Выберите наибольшее из записанных ниже чисел.
1) b — .
2) a — .
3) a : b
4) a + b
3. Каждое из записанных ниже выражений умножили на число ![]() Для какого выражения было получено рациональное произведение?
Для какого выражения было получено рациональное произведение?

4. Решите уравнение 2х2 + 7х + 5 = 0.
Ответ: _________________.
5. Установите соответствие между графиками функций и формулами, которые их задают (см. рис. 25).
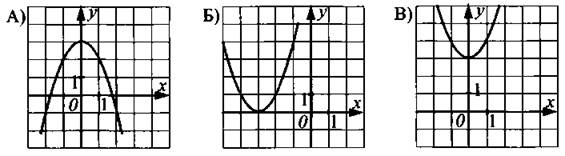
Рис. 25
1) у = (х + 3)2
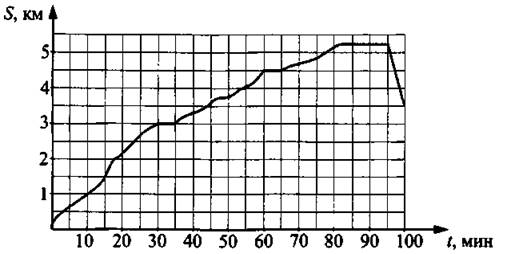
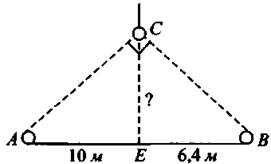
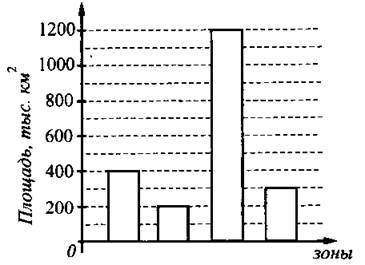
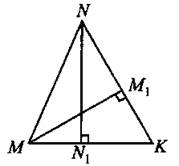
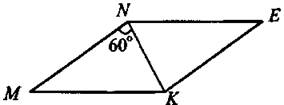
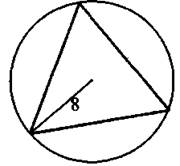
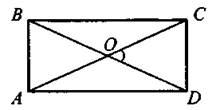
2) у = (х — 3)2 3) у = х2 + . 4) у = —х2 + 3 Ответ: 6. Найдите знаменатель геометрической прогрессии, если все её члены положительные, четвёртый и шестой члены равны 0,01 и 1 соответственно. Ответ: _________________. 7. Упростите выражение (с — 4)(с — 2) — с(с — 6) и найдите его значение при с = 0,17. Ответ: _________________. 8. Решите систему неравенств На какой из координатных прямых изображено множество её решений? Модуль «Геометрия» 9. В ромбе MNEK величина угла MNK равна 60° (см. рис. 26). Найдите величину угла МКЕ. Ответ дайте в градусах. Рис. 26 Ответ: _________________. 10. В равностороннем треугольнике АВС радиус описанной окружности равен 8 см (см. рис. 27). Найдите (в см) радиус вписанной окружности. Рис. 27 Ответ: _________________. 11. Найдите площадь прямоугольника (см. рис. 28), у которого диагональ равна 6 см, а синус угла между диагоналями равен 0,4. Рис. 28 Ответ: _________________. 12. Найдите длину вектора Ответ: _________________. 13. Укажите номера верных утверждений. 1) Если в равнобедренном треугольнике угол при основании острый, то такой треугольник — остроугольный. 2) В прямоугольном треугольнике тангенсом острого угла α называется отношение 3) Во всяком треугольнике биссектриса угла равна его медиане. Ответ: _________________. Модуль «Реальная математика» 14. Маша купила круассан и разделила его между собой и подружками. Она сделала 3 разлома. На сколько кусков Маша разделила круассан? Ответ: _________________. 15. На графике показана зависимость пройденного пешеходом расстояния от времени (см. рис. 29). По горизонтали откладывается время в минутах, по вертикали — расстояние в километрах. Сколько минут пешеход отдыхал второй раз? Рис. 29 Ответ: _________________. 16. Саша участвовал в школьном конкурсе «Умники и умницы». В первом туре предлагались задания по физике, алгебре и геометрии. При этом 20% всех заданий были по геометрии, восьмая часть оставшихся — по физике и 28 по алгебре. Сколько заданий в первом туре? Ответ: _________________. 17. Лучи от двух источников света A и В, установленных на сцене, освещают гимнастку, работающую на подвешенном кольце С (см. рис. 30). На какой высоте (в м) будет находиться гимнастка в момент, когда угол между лучами будет 90°, если АЕ = 10 м, BE = 6,4 м? Рис. 30 Ответ: _________________. 18. На диаграмме (см. рис. 31) показано распределение по площадям таёжной, тундровой, лесостепной и горной зон в Западной Сибири (в тыс. км2). Известно, что площадь таёжной зоны в 3 раза больше, чем лесостепной, и на 900 тыс. км2 больше, чем тундровой. Определите, на сколько км2 горная зона меньше тундровой. Рис. 31 Ответ: _________________. 19. В чемпионате мира участвуют 10 команд. С помощью жребия их нужно разделить на пять групп по 2 команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 2, 2, 3, 3, 4, 4, 5, 5. Капитаны команд будут тянуть по одной карточке. Какова вероятность того, что команда из России окажется в первой группе? Ответ: _________________. 20. Дана формула мощности N = A/t, где А — работа (в джоулях), t — время (в секундах). Найдите t, если N = 5 Вт, А = 20 Дж. Ответ: _________________. Часть 2 Задания этой части выполняйте с записью решения Модуль «Алгебра» 21. Решите неравенство (х — 10) (x + 2) ≤ 160. 22. От пристани А к пристани В, расстояние между которыми 60 км, отправился с постоянной скоростью первый теплоход, а через час после этого вслед за ним со скоростью на 10 км/ч больше отправился второй. Найдите скорость второго теплохода, если в пункт В он прибыл одновременно с первым. Ответ дайте в км/ч. 23. Найдите все значения а, при которых прямая, проходящая через точки (0; 3) и (а; 0), имеет с графиком функции у = -3/x только одну общую точку. Модуль «Геометрия» 24. Медиана, проведённая к гипотенузе прямоугольного треугольника, равна 6 и делит прямой угол в отношении 1:2. Найдите катеты треугольника. 25. В остроугольном треугольнике MNK (см. рис. 32) проведены высоты ММ1 и NN1. Докажите, что М1К ∙ NK = N1K ∙ МК. Рис. 32 26. В треугольнике АВС точки М и N — середины сторон АВ и АС соответственно. Найдите радиус окружности, вписанной в треугольник АВС, если АВ = 17 см, АС = 9 см, MN = 5 см.
![]()

![]()
![]()