Поурочные разработки по Геометрии 11 класс
Объем пирамиды - урок 2 - Объем наклонной призмы, пирамиды и конуса - ОБЪЕМЫ ТЕЛ
Цели урока:
- сформировать навык нахождения объема пирамиды, у которой вершина проецируется в центр вписанной или описанной около основания окружности.
Ход урока
I. Проверка вывода формулы для вычисления объема усеченной пирамиды (ученик у доски)
Ответ ученика:
Объем усеченной пирамиды рассматриваем как разность объемов полной пирамиды и той, что отсечена от нее плоскостью, параллельной основанию (рис. 1).
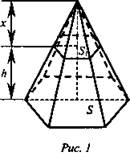
Поэтому,
![]()
Из равенства ![]() Находим:
Находим: ![]() Подставляем это выражение для х в формулу (1),
Подставляем это выражение для х в формулу (1),

II. Устная работа в форме теста, с проверкой у доски.
1. В наклонной призме боковое ребро равно 7 см, перпендикулярное сечение - прямоугольный треугольник с катетами: 4 см и 3 см. найдите объем призмы.
а) 10 см3, б) 42 см3, в) 60 см3, г) 30 см3.
2. В правильной шестиугольной пирамиде сторона ее основания 2 см, объем пирамиды 6 см3. Чему равна высота?
а) √3 см, б) 3 см, в) 1/3 см.
3. Объем пирамиды равен 56 см3, площадь основания 14 см2. Чему равна высота?
а) 14 см, б) 12 см, в) 16 см.
4. В правильной треугольной пирамиде высота равна 5 см, стороны основания 3 см. Чему равен объем пирамиды?
![]()
5. В правильной четырехугольной пирамиде высота равна 9 см. Сторона основания 4 см. найдите объем пирамиды.
а) 50 см3, б) 48 см3, в) 16 см3.
6. Объем правильной четырехугольной пирамиды равен 27 см3, высота 9 см. найти сторону основания.
а) 12 см, б) 9 см, в) 3 см.
7. Объем усеченной пирамиды равен 210 см3, площадь нижнего основания 36 см2, верхнего 9 см2. Найдите высоту пирамиды.
а) 1 см, б) 15 см, в) 10 см.
8. Равновеликие призма и правильная четырехугольная пирамида имеют равные высоты.
Чему равна сторона основания пирамиды, если площадь основания призмы равна S?
![]()
Таблица ответов.
Задача |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
б |
а |
б |
а |
б |
в |
в |
в |
III. Решение задач
Рассмотрим базовые задачи (повторение).
Задача № 1.
Если боковые ребра пирамиды равны (или составляют равные углы с плоскостью основания), то вершина пирамиды проецируется в центр окружности, описанной около основания (рис. 2).
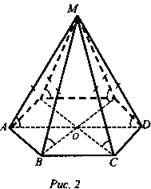
Доказательство:
1) ΔМАО = ΔМВО = ΔМСО = ... (равны по катету и гипотенузе или по катету и острому углу).
2) Тогда ОА = ОВ = ОС = ..., т.е. точка О - центр окружности, описанной около основания.
Задача № 2.
Если двугранные углы при основании пирамиды равны (или равны высоты боковых граней, проведенные из вершины пирамиды), то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды (рис. 3).
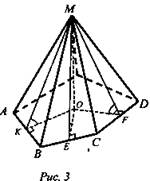
Доказательство:
1) ΔМКО = ΔМЕО = ΔMFO = ... (по катету и острому углу).
2) OK = OE = OF =..., т.е. точка О - центр окружности, вписанной в основание пирамиды.
Решаем задачи по готовым чертежам:
1. Дано: ABCD - пирамида. ΔАВС - прямоугольный, ∠С = 90°, АС = 6, ВС = 8. Каждое боковое ребро составляет с плоскостью основания угол 45° (рис. 4).
Найти: Vпир. - ?
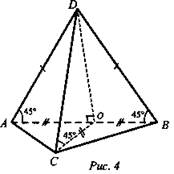
Решение:
1) Так как α = 45°, то вершина пирамиды проецируется в центр окружности, описанной около основания. ΔАВС - прямоугольный, значит, точка О - середина гипотенузы, АО = ОС = ОВ.
2) ΔАВС, ∠С = 90°, тогда по теореме Пифагора: ![]() АВ = 10, АО = 5.
АВ = 10, АО = 5.
3) ΔAOD: ∠О = 90°, ∠D = ∠А = 45°, DO = OA = 5.
4) ![]()
5) ![]() так как H = DO.
так как H = DO.
(Ответ: 40.)
2. Дано: ABCD - пирамида. ΔАВС - равнобедренный. АВ = АС = 10, ВС = 12. AD = BD = CD = 15 (рис. 5).
Найти: V - ?
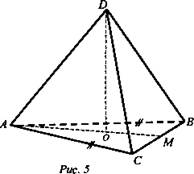
Решение:
1) Так как AD = BD = CD = 15, то вершина пирамиды проецируется в центр окружности, описанной около основания, значит, R = AO.
2) ![]() тогда
тогда ![]()
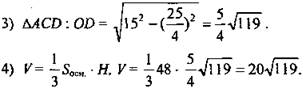
(Ответ: 20√119.)
Решение задач из учебника: № 695 (а, б).
Задача № 695 а). Дано: SABС - пирамида, ∠CAB = 90°, ВС = С, ∠ABC = φ, ∠SCO = Q (рис. 6).
Найти: Vпир. - .
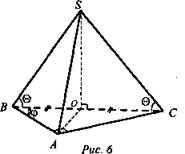
Решение:
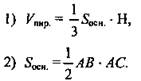
Рассмотрим ΔABC: ![]() Тогда
Тогда ![]()
3) Так как точка О - центр окружности, описанной около основания, и ОВ = ОС = ОА, то SA = SB = SC.
4) ![]() значит,
значит, ![]()
5) ![]()
(Ответ: ![]() )
)
Задача 695 б). Дано: ABCD - пирамида. ΔABC - равнобедренный. AB = AC = 10; BC = 12. ∠DMO = 45° (рис. 7).
Найти: Vпир. - ?
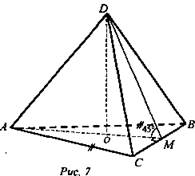
Решение:
1) ![]() где
где ![]() точка О - центр вписанной в основание окружности.
точка О - центр вписанной в основание окружности.
2) SΔ = 48 (смотри предыдущую задачу, формула Герона). r = S/P; r = 48/16 = 3;
3) ΔDOM: OD = ОМ = 3, т. к. ∠ODM = 45°.
4) ![]()
(Ответ: 48.)
IV. Подведение итогов
- Что необходимо знать, чтобы определить объем пирамиды?
Домашнее задание
П. 69, № 695 в), 697, 690.