Поурочные разработки по Геометрии 11 класс
Координаты вектора - урок 2 - Координаты точки и координаты вектора - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
Цели урока:
- отработка умений и навыков действий над векторами с заданными координатами;
- контроль знаний и умений учащихся в ходе выполнения самостоятельной работы.
Ход урока
I. Организационный момент
Учитель сообщает тему, цель и план урока.
II. Актуализация знаний, умений и навыков учащихся
1. Двое учащихся у доски доказывают правила действий с векторами (1; 2) и (3; 4).
2. С остальными учащимися проводится математический диктант.
Вопросы:
1) Укажите координаты векторов ![]()
2) На какой координатной оси или в какой координатной плоскости лежат точки, если а) А(2; 3; 0), б) В(0; 0; 4), в) С(3; 0; 1); а) М(0; 8; 0), б) N(0; 2; 6), в) K(-7; 0; 7)?
(Ответ: а) А ∈ (хОу) б) В ∈ (xOz), В ∈ (yOz), В ∈ Oz ; в) С ∈ (xOz); а) М ∈ (xOy), М ∈ (yOz), M ∈ Oy б) N ∈ (yOz), в) K ∈ (xOz).)
3) Записать разложение векторов ![]()
![]()
Решение: ![]()
4) Записать координаты векторов ![]() если
если
![]()
Решение: n{3; 2; -1}, m{0; 1; 0,8}; n{5; -1; 0}, m{2; 1; -7}.
5) В какой координатной плоскости лежит вектор ![]() если
если ![]()
Решение: ![]() то есть
то есть ![]() то есть
то есть ![]()
6) На какой координатной оси лежит вектор ![]() если
если ![]()
Ответы: ![]()
Верные ответы можно заготовить заранее на запасной доске (или показать через кодоскоп) и осуществить взаимопроверку.
По окончании математического диктанта заслушиваются доказательства правил действий над векторами с заданными координатами.
Дополнительные вопросы отвечающим у доски:
1) Какие векторы называются коллинеарными?
2) Дайте определение средней линии треугольника.
1) Какие векторы называются компланарными?
2) Расскажите теорему о средней линии треугольника.
III. Отработка знаний, умений и навыко.
Задача № 410 (решается у доски)
Дано: ![]()
Найти: ![]()
Решение:
![]()
![]()
![]()
Задача № 408 (решается у доски)
Дано: ОА = 4, ОВ = 9, ОС = 2, М, N, Р - середины отрезков АС, ОС, СВ (рис. 6).
Найти: координаты векторов ![]()
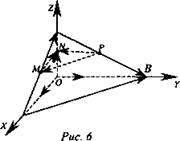
Решение:
Р - середина ВС; N - середина ОС; М - середина АС.
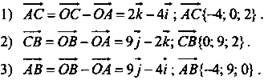
4) MN - средняя линия ΔАОС, значит, ![]()
5) NP - средняя линия ΔСОВ, значит, ![]()

Задача № 414 (а) (решается у доски)
Дано: ![]() - коллинеарные.
- коллинеарные.
Найти: m; n.
Решение: Так как ![]() коллинеарные и
коллинеарные и ![]() то существует число k такое, что
то существует число k такое, что ![]() и обратно. Если существует число k, такое что
и обратно. Если существует число k, такое что ![]() , то
, то ![]() коллинеарные. Найдем числа m, n и k, чтобы
коллинеарные. Найдем числа m, n и k, чтобы ![]() . Используя условие, имеем:
. Используя условие, имеем: ![]()
![]() Итак, векторы
Итак, векторы ![]() коллинеарные, если m = 10, n = 6/5. (Ответ: m = 10, n = 6/5.)
коллинеарные, если m = 10, n = 6/5. (Ответ: m = 10, n = 6/5.)
IV. Самостоятельная работа (см. приложение)
Ответы:
Вариант А 1: 1. ![]()
Вариант А 2: 1. ![]()
Решение:
Вариант Б 1: ![]()
![]()
![]()
Вариант Б 2: ![]()
![]()
![]()
Вариант В 1: ![]()
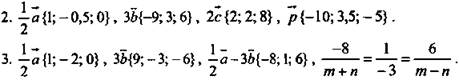
Вариант В 2: ![]()
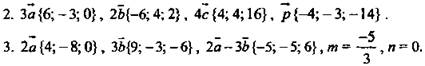
V. Итог урока
- В ходе урока мы повторили правила действий над векторами и проверили усвоение данной темы.
Домашнее задание
№ 409 (в, е, ж, и, м); 41.
(2 пункта по выбору учащихся).