Поурочные разработки по Геометрии 11 класс
Касательная плоскость к сфере - Сфера - ЦИЛИНДР, КОНУС И ШАР
Цели урока:
- рассмотреть теоремы о касательной плоскости к сфере;
- научиться решать задачи по данной теме.
Ход урока
I. Организационный момент
II. Актуализация знаний учащихся
1. Устный опрос учащихся.
а) Что называется сферой? .
Поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, называемой центром сферы, а данное расстояние - радиусом.
б) Что называют диаметром сферы?
Отрезок, соединяющий две точки сферы и проходящий через центр.
в) Расскажите о взаимном расположении сферы и плоскости.
Пусть R - радиус, d - расстояние от центра сферы до плоскости. Возможны случаи:
1. d < R: сфера и плоскость пересекаются по окружности;
2. d = R: сфера и плоскость имеют одну общую точку;
3. d > R: сфера и плоскость не имеют общих точек.
2. Проверка домашнего задания:
Ученики работают у доски:
I ученик.
а) вывод уравнения сферы.
Пусть точка С(x0; у0; z0) центр данной сферы, а точка М(х; у; z) лежит на сфере (рис. 1).
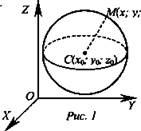
1. Найдем расстояние между этими точками: ![]() но МС есть радиус сферы, значит, можно записать:
но МС есть радиус сферы, значит, можно записать: ![]() или
или ![]() - уравнение сферы с центром в точке С (x0; у0; z0).
- уравнение сферы с центром в точке С (x0; у0; z0).
2. Если центр сферы совпадет с началом отсчета данной системы координат, то уравнение сферы будет иметь вид: R2 = х2 + у2 + z2, так как х0 = 0, у0 = 0, z0 = 0.
II ученик
б) проверка домашних задач № 581, № 586 (б), № 587 с записью на доске.
№ 581. Дано: ΔABC, вершины А, В, С лежат на сфере с центром в точке О. Радиус R = 13 см, АВ = 6 см, ВС = 8 см, АС = 10 см (рис. 2).
Найти: d - расстояние от центра сферы до плоскости ΔABC.
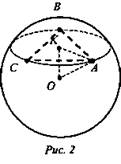
Решение: Плоскость ΔАВС пересекает сферу по окружности, которая будет описанной около ΔАВС. Из точки О проведем ОК перпендикулярно плоскости ABC. OK = d будет искомым расстоянием, а точка К - центром описанной около ΔАВС окружности. Тогда отрезок АК - радиус описанной около ΔАВС окружности, а АО - радиус сферы.
Рассмотрим прямоугольный ΔОКА: ![]()
![]() по теореме Пифагора.
по теореме Пифагора. ![]() - описанной окружности.
- описанной окружности. ![]() найдем площадь ΔАВС по формуле Герона.
найдем площадь ΔАВС по формуле Герона. ![]()
![]()
![]() (Ответ: 12 см.)
(Ответ: 12 см.)
III ученик
№ 586 б) Дано: ОАВС - тетраэдр, ОН - высота, сфера с центром в точке О и радиусом R; R = 3 м, ОН = 95 см (рис. 3).
Найти: взаимное расположение сферы и плоскости ΔАВС.
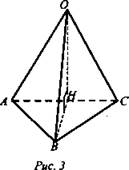
Решение: Пусть ОН = d— расстояние от центра сферы до плоскости ΔАВС. R > d, R2 – d > 0. х2 + у2 = R2 - d2 - уравнение окружности на плоскости ABC. Значит, сфера и плоскость основания тетраэдра пересекаются по окружности. (Ответ: сфера и плоскость пересекаются по окружности.)
IV ученик
№ 587. Дано: шар с центром в точке О, радиусом R, d — расстояние от центра О до секущей плоскости; а) R = 12 см, d= 8 см. б) Sсеч. = 12 см2, d= 2 см (рис. 4).
Найти: a) Sсеч.; б) R.
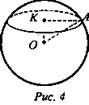
Решение: а) Шар и плоскость пересекаются по окружности радиуса ![]()
![]() В сечении получится круг площадью
В сечении получится круг площадью ![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
V ученик.
в) решение дополнительной задачи.
Диаметр шара 16 см. Через конец диаметра под углом 60° проведено сечение шара плоскостью. Найдите площадь сечения.
Дано: шар с центром в точке О, диаметр d = 16 см, угол между диаметром и сечением шара плоскостью 60° (рис. 5).
Найти. Sсеч.
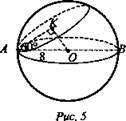
Решение: Пусть d = АВ · ОК - расстояние от О до плоскости. Рассмотрим ΔАОК: ![]() (радиус сферы), ∠АОК = 90° (ОК - расстояние от центра до плоскости сечения). Sсеч. = πr2, где r – радиус сечения, r = АК = 1/2 · АО = 1/2 · 8 = 4 (см) как катет, лежащий против угла в 30°. Sсеч. = π · 42 = 16π (см2). (Ответ: 16π см2.)
(радиус сферы), ∠АОК = 90° (ОК - расстояние от центра до плоскости сечения). Sсеч. = πr2, где r – радиус сечения, r = АК = 1/2 · АО = 1/2 · 8 = 4 (см) как катет, лежащий против угла в 30°. Sсеч. = π · 42 = 16π (см2). (Ответ: 16π см2.)
3. Работа с чертежами.
Найдите площадь сечения плоскостью α шара с центром в точке О.
Сечение есть круг с центром в точке А и радиусом АВ. ОА ⊥ α.
В ΔОАВ ∠A = 90°, r = АВ =![]() = 40 (см2) по теореме Пифагора
= 40 (см2) по теореме Пифагора
Sсеч. = πr2 = π · 402 = 1600π (см2)

III. Изучение нового материала (рис. 7)
1. Повторение изученного в курсе планиметрии:
а) Что называется касательной к окружности? Прямая, имеющая с окружностью одну общую точку.
б) Вспомним основные теоремы.
1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
2) Если прямая проходит через конец радиуса, лежащей на окружности, и перпендикулярна к этому радиусу, то она является касательной.
3) Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
2. Доказательство основных теорем о касательной плоскости.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка - точкой касания.
Теорема: (свойство касательной плоскости)
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Дано: сфера с центром в точке О и радиусом R, α - касательная плоскость, А - точка касания (рис. 8).
Доказать: R ⊥ α.
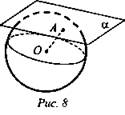
Доказательство: Предположим противное: пусть R = ОA ⊥ α, следовательно ОА - наклонная к плоскости α, значит, расстояние от центра, сферы до плоскости α меньше R = OA: d < R, значит, сфера и плоскость а пересекают по окружности, что противоречит условию, что α - касательная плоскость, т.е. плоскость α и сфера имеют одну общую точку. Значит, R ⊥ α.
Теорема: (признак касательной плоскости)
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
Дано: сфера с центром в точке О и радиусом R, R ⊥ α, ОА = R, А лежит на сфере.
Доказать: α - касательная плоскость.
Доказательство: Радиус перпендикулярен к данной плоскости R ⊥ α, значит, расстояние от центра сферы до плоскости равно радиусу сферы d = R, следовательно, сфера и плоскость имеют только одну общую точку, то есть данная плоскость является касательной.
IV. Закрепление изученного материала
Задача № 592. Дано: сфера с центром в точке О и радиусом R, R = 112 см, α - касательная, А - точка касания, Р лежит на сфере, АР = 15 см. М - точка пересечения РО и сферы (рис. 9).
Найти: РМ.
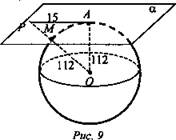
Решение: ΔОАР - прямоугольный, так как ОА = R, α - касательная плоскость. По теореме Пифагора найдем ![]() PM = OD – R = 113 – 112 = 1 (см). (Ответ: 1 см.)
PM = OD – R = 113 – 112 = 1 (см). (Ответ: 1 см.)
V. Подведение итогов
1. Вспомним понятие касательной плоскости к сфере.
2. Свойство касательной плоскости.
3. Признак касательной плоскости.
Домашнее задание
Пп. 58-61, вопросы 7-9 к главе VI.
I уровень
Задача. Дан шар с центром в точке О, α - касательная плоскость, точка А - точка касания, точка В лежит на плоскости α, АВ = 21 см, ВО = 29 см (рис. 10).
Найдите радиус шара.
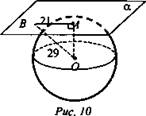
Дано: шар с центром в точке О, α - касательная плоскость, А - точка касания, ОВ = 29, АВ = 21 см.
Найти: R шара.
Решение: R = OA, так как А - точка касания, рассмотрим прямоугольный ΔОАВ (α - касательная плоскость, А - точка касания, значит ОА ⊥ α): по теореме Пифагора найдем ![]() (Ответ: 20 см.)
(Ответ: 20 см.)
II уровен.
Задача № 591.
Решение см. урок № 25.