Параллельность прямых и плоскостей - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ

Цель урока:

- повторить определения параллельных прямых, прямой и плоскости; основные свойства, связанные с этими определениями.

Ход урока

I. Проверка домашнего задания

II. Решение задач

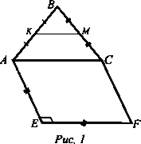
1. По готовому рисунку (устно): а) докажите, что КМ || EF; б) найдите КМ, если EF = 8 см (рис. 1).

Решение:

а) КМ - средняя линия ΔАВС, значит, КМ || AC; ACFE - квадрат, значит AC || EF; КМ || АС; EF || АС, значит, КМ || EF (если две прямые параллельны третьей, то они параллельны);

б) (по свойству средней линии); КМ = 4 см.

- Какие прямые называются параллельными в пространстве? (если они лежат в одной плоскости и не пересекаются). Привести примеры.

2. ABDC - трапеция, AD ⊂ α,E и F - середины АВ и CD соответственно. Докажите, что EF || α (рис. 2).

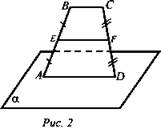
Решение: EF - средняя линия трапеции ABCD; EF || AD, AD ⊂ α, значит, EF || α (если прямая, не лежащая в плоскости параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости).

- Какая прямая называется параллельной плоскости? (Прямая и плоскость называются параллельными, если они не имеют общих точек.) Привести примеры.

3. Через вершины А и С параллелограмма ABCD проведены параллельные прямые А1А и С1С, не лежащие в плоскости параллелограмма.

Докажите параллельность плоскостей А1АВ и C1CD (рис. 3).

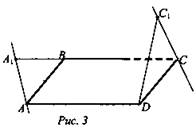
Решение: АА1 || СС1 по условию; АВ || CD по определению параллелограмма; (A1AB) || (С1CD) по признаку параллельности плоскостей (Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.)

- Какие плоскости называются параллельными? (Если они не пересекаются.) Привести примеры.

Задача (письменно)

Концы двух пересекающихся отрезков AC || BD лежат на двух параллельных плоскостях, причем расстояния между точками одной плоскости равны.

а) Докажите, что АВ || CD; б) Один из углов четырехугольника ABCD равен 65°. Найдите остальные углы.

Дано: АВ = DC, ∠ADC = 65° (рис 4).

Доказать: АВ || CD.

Найти: а) углы четырехугольника ABCD.

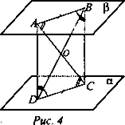
Доказательство:

1. значит, существует γ, {АС, DB} ⊂ γ.

2.

3. DC || АВ по свойству параллельных плоскостей 1 (если две параллельные плоскости параллельны третьей, то линии их пересечения параллельны);

б) Решение:

1. ΔAOB = ΔCOD (II признак: АВ = DC по условию, ∠ODC = ∠OBA, ∠OCD = ∠OAD - внутренние накрест лежащие для АВ || DC и секущих АВ, АС).

2. АО = ОС, OD = ОВ.

3. ΔAOD = ΔСОВ (I признак: DO = ОВ, АО = ОС, ∠AOD = ∠COB - вертикальные).

4. ∠ODA = ∠OBC, значит, AD || ВС, так как это внутренние накрест лежащие углы для прямых AD и ВС и секущей DB.

5. ADCB - параллелограмм по определению.

6. ∠D = ∠B, ∠A = ∠C, ∠D + ∠A = 180°. Если ∠D = 65°, то ∠B = 65°, ∠A = ∠C = 180° - 65° = 115°. (Ответ: ∠A = ∠C = 115°, ∠D = ∠B = 65°.)

III. Подведение итогов

Учащиеся отвечают на вопрос: «Какие определения и свойства, связанные с понятием параллельности, сегодня прозвучали?».

Домашнее задание

С. 32, вопросы 1-3, 5, 7, 11; № 99 (или № 103 дополнительно).

№ 99. Дано: (рис 5).

Доказать:

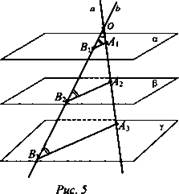
Доказательство:

1. Так как а ∩ в, то

2. В1А1 || В2А2 || B3А3 по свойству 1.

3. ΔОВ1А1 ~ ΔОВ2А2 ~ ΔОВ3А3 (по двум углам).

4.

№ 103. Дано: ABCD - тетраэдр М ∈ AD, Р ∈ DC, N ∈ DB; (рис. 6).

Доказать: (MNP) || (ABC).

Найти: SΔMNP, если SΔABC = 10 см2 и

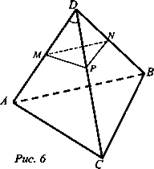
Доказательство:

1. Если то

2. ΔMDP ~ ΔADC (по пропорциональности двух сторон и ∠D общий); ΔPDN ~ ΔCDB, ΔMND ~ ΔABD.

3. ∠DMP = ∠DAC - соответственные для МР и АС и секущей AD. Значит, МР || АС. Аналогично, PN || СВ, MN || АВ.

4. (MNP) || (АСВ) по свойству параллельности плоскостей.

Решение:

1.

2. ΔMPN ~ ΔACB (по пропорциональности трех сторон); k = 2/3.

3. (Ответ: )