Вариант № 30 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. При оплате услуг через платёжный терминал взымается комиссия 6%. Терминал принимает суммы, кратные 10 рублям. Вася хочет положить на счёт своего мобильного телефона не меньше 500 рублей. Какую минимальную сумму (в рублях) он должен положить в приёмное устройство данного терминала?

В2. На графике (рис. 163) изображена зависимость крутящего момента двигателя от числа оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н∙м. Скорость автомобиля (в км/ч) приближённо выражается формулой v = 0,045п, где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не менее 80 Н∙м? Ответ дайте в километрах в час.

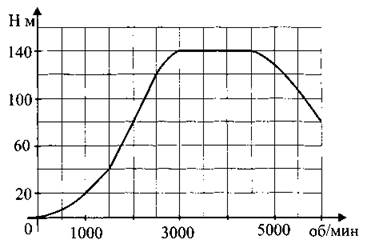
Рис. 163.

В3. Площадь параллелограмма ABCD равна 24. Точка М — середина стороны DA. Найдите площадь трапеции АМСВ.

В4. В таблице даны условия банковского вклада в трёх различных банках. Предполагается, что клиент кладёт на счёт 20000 рублей сроком на 1 год. В каком банке к концу года вклад окажется наибольшим? В ответе укажите сумму этого вклада в рублях.

Банк	Обслуживание счёта*	Процентная ставка (% годовых)**
Банк А	150 руб. в год	4
Банк Б	Бесплатно	2
Банк В	10 руб. в месяц	3

* В начале года или месяца со счёта снимается указанная сумма в уплату за ведение счёта.

** В конце года вклад увеличивается на указанное число процентов.

В5. Найдите корни уравнения В ответе запишите наибольший отрицательный корень.

В6. Найдите косинус угла MON. В ответе укажите значение косинуса, умноженное на 3√2 (см. рис. 164).

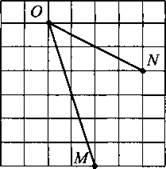
Рис. 164.

В7. Найдите f(3х + 4) + f(4 – 3x), если

В8. Прямая у = 6x + 5 является касательной к графику функции у = 3х² + bх + 17. Найдите b, учитывая, что абсцисса точки касания меньше 0.

В9. В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ АС₁ = 2ВС. Найдите угол между прямыми BD₁ и СА₁. Ответ дайте в градусах.

В10. В торговом центре два одинаковых автомата продают шоколадки. Вероятность того, что к концу дня в автомате закончатся шоколадки, равна 0,4. Вероятность того, что шоколадки закончатся в обоих автоматах, равна 0,18. Найдите вероятность того, что к концу дня шоколадки останутся в обоих автоматах.

В11. Объём треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 2 (см. рис. 165). Найдите объём шестиугольной пирамиды.

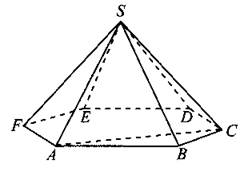
Рис. 165.

В12. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону U = U₀sin(ωt + φ), где t — время в секундах, амплитуда U₀ = 10 В, частота ω = 100°/с, фаза φ = 0°. Датчик настроен так, что если напряжение в нём не ниже, чем 5 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

В13. Грузовой автомобиль перевозит технику из одного города в другой, каждый день проезжая на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый день грузовой автомобиль прошёл 520 км. Определите, сколько километров проехал грузовой автомобиль за третий день, если весь путь он проделал за 5 дней и расстояние между городами составляет 3270 км.

В14. Найдите наименьшее значение функции у = 11 sinx — 13х + 5 на отрезке [-π/2; 0].

Часть 2

С1. Решите уравнение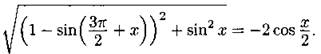

С2. В треугольной пирамиде SABC все углы при вершине С прямые, SC = 4, АС = ВС = 3. На рёбрах SA и SB взяты точки М и N соответственно, так что Найдите косинус угла между прямыми СМ и CN.

С3. Решите систему неравенств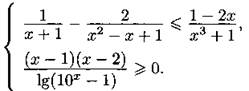

С4. Окружность радиуса 10 вписана в угол 60°. Вторая окружность также вписана в этот угол и пересекается с первой в точках А и В. Расстояние между центрами окружностей равно 12. Найдите АВ.

С5. При каких а уравнение имеет ровно одно решение?

С6. Решите в целых числах уравнение