Вариант № 26 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Клиент взял в банке кредит на сумму 18000 рублей на год под 15% годовых. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму вместе с процентами. Сколько рублей клиент должен вносить в банк ежемесячно?

В2. На рисунке 147 точками показано количество золотовалютных резервов в России за период с 10 по 20 февраля 2011 года. По горизонтали указываются числа месяца, по вертикали — количество золотовалютных резервов в миллиардах долларов США. Для наглядности точки соединены линией. Определите по рисунку разность между наибольшим и наименьшим количествами золотовалютных резервов в период с 11 по 17 февраля (в миллиардах долларов США).

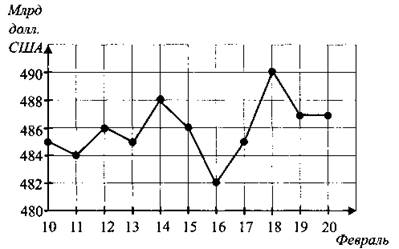
Рис. 147.

В3. Найдите площадь фигуры (в см²), изображённой на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите результат S/π (см. рис. 148).

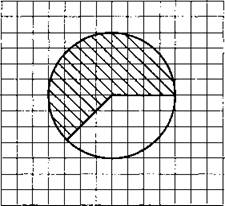
Рис. 148.

В4. Строительной фирме нужно приобрести 135 тонн камня у одного из трёх поставщиков. Какова наименьшая стоимость такой покупки с доставкой (в рублях)? Цены и условия доставки приведены в таблице.

Поставщик	Цена камня (руб. за тонну)	Стоимость доставки (руб)	Дополнительные условия
А	1800	17000	При заказе с доставкой на сумму свыше 200 000 рублей предоставляется скидка 15%
Б	1700	10500	При заказе на сумму свыше 200 000 рублей доставка бесплатно
В	1600	14000	При заказе на сумму свыше 240 000 рублей доставка бесплатно

В5. Найдите корень уравнения

В6. Углы А, В, С четырёхугольника ABCD, вписанного в окружность, относятся как 3:2:7. Найдите больший угол этого четырёхугольника (в градусах).

В7. Найдите tg α, если

B8. На рисунке 149 изображён график функции у = F(x), одной из первообразных некоторой функции f(x), определённой на интервале (—6; 2). Пользуясь рисунком, определите количество решений уравнения f (x) = 0 на отрезке [—5; 1].

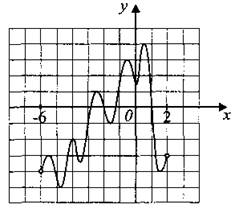
Рис. 149.

В9. Найдите угол ABD₁ прямоугольного параллелепипеда, для которого АВ = 8, AD = 4√3, АА₁ = 12 (см. рис. 150). Ответ дайте в градусах.

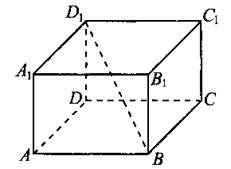
Рис. 150.

В10. На концерте выступают группы музыкантов — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из России будет выступать после группы из Франции и после группы из Италии? Результат округлите до сотых.

В11. Основанием пирамиды служит квадрат, одна боковая грань перпендикулярна плоскости основания, а две смежные боковые грани, имеющие с ней общее ребро, наклонены к плоскости основания под углом 30° (см. рис. 151). Высота пирамиды равна 3. Найдите объём пирамиды.

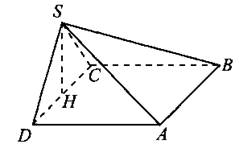
Рис. 151.

В12. Мяч бросили под углом α к плоской горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле При каком наименьшем значении угла а (в градусах) время полёта будет не меньше 2 секунд, если мяч бросают с начальной скоростью v₀ = 20 м/с? Считайте, что ускорение свободного падения g = 10 м/с².

В13. Ремонт одной и той же квартиры Виктор и Алексей делают за 8 дней, как и Андрей вместе с Виктором, при этом Алексей с Андреем могут выполнить этот ремонт за 12 дней. Сколько дней будет длиться ремонт, если все 3 мастера будут работать одновременно?

В14. Найдите наибольшее значение функции у = 2 sin х — 2х cos х — 0,5х² на отрезке [-π/2; π/6].

Часть 2

С1. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку [-5π/2; -5].

С2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ через вершину А проведена секущая плоскость, пересекающая ребро СС₁ в точке Е так, что получившееся сечение — ромб, площадь которого равна 11. Найдите отношение ЕС : СС₁, если АВ = ВС = 3 и АА₁ = 5.

С3. Решите систему неравенств

С4. В треугольнике АВС с углом В, равным 45°, и стороной СВ = 8 АН — высота. Прямая AH пересекает описанную около треугольника окружность в точке D. Площадь треугольника CADравна 12. Найдите АС.

С5, Найдите все такие значения параметра а, что каждое число, являющееся корнем уравнения при этом значении а, не будет корнем при любом другом значении параметра.

С6. В коробке находится 80 шариков нескольких цветов. Среди любых тринадцати шариков, взятых наугад, обязательно окажется четыре шарика одного цвета.

а) Обязательно ли среди шариков в коробке имеется 20 шариков одного цвета?

б) Какое максимальное число шариков можно удалить из коробки, чтобы, не нарушив условия задачи (об обязательном присутствии четырёх шариков одного цвета среди любых тринадцати, взятых наугад), можно было утверждать, что в коробке имеется 19 шариков одного цвета?

в) Какое минимальное число шариков нужно добавить в коробку, чтобы, не нарушив условия задачи (об обязательном присутствии четырёх шариков одного цвета среди любых тринадцати, взятых наугад), можно было утверждать, что в коробке находится 21 шарик одного цвета?