Математика сборник задач для подготовки к ЕГЭ
Вариант № 5 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ
Часть 1
В1. В школе есть трёхместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвуют 25 человек?
В2. На рисунке 39 точками показано суточное количество осадков, выпадавших с 11 по 23 сентября. По горизонтали указываются числа месяца, по вертикали — количество осадков в миллиметрах, выпавшее в соответствующий день. Для наглядности точки на рисунке соединены линией. Определите по рисунку, сколько миллиметров осадков выпало 17 сентября.
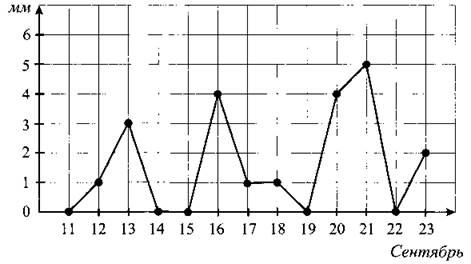
Рис. 39.
В3. На клетчатой бумаге с клетками размером 1 см х 1 см изображён треугольник (см. рис. 40). Найдите его площадь в квадратных сантиметрах.
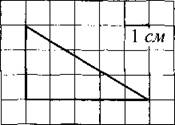
Рис. 40.
В4. От дома до дачи можно доехать на автобусе, на электричке или на маршрутном такси. В таблице показано время, которое нужно затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Ответ дайте в минутах.
|
|
1 |
2 |
3 |
|
1. Автобус |
От дома до автобусной станции — 10 мин. |
Автобус в пути: 1 ч 25 мин. |
От остановки автобуса до дачи пешком — 25 мин. |
|
2. Электричка |
От дома до станции железной дороги — 40 мин. |
Электричка в пути: 55 мин. |
От станции до дачи пешком — 30 мин. |
|
3. Маршрутное такси |
От дома до остановки маршрутного такси — 35 мин. |
Маршрутное такси в пути: 3/4 ч. |
От остановки маршрутного такси до дачи пешком — 35 мин. |
В5. Найдите корень уравнения ![]()
В6. В треугольнике АВС угол С равен 90°, cos В = 0,5, АВ = 16. Найдите ВС.
В7. Найдите значение выражения ![]()
В8. На рисунке 41 изображены график функции у = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
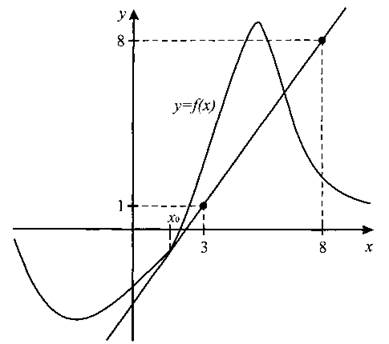
Рис. 41.
В9. Найдите квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда ABCDA1B1C1D1 (см. рис. 42), если АВ = 8, AD = 3, АА1 = 5.
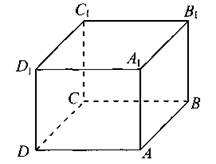
Рис. 42.
В10. Вася, Петя, Дима, Коля и Андрей тянут жребий, кому идти в магазин за продуктами. Найдите вероятность того, что поход за продуктами выпадет Диме.
B11. Прямоугольный параллелепипедописан около цилиндра, радиус основания и высота которого равны 1. Найдите объём параллелепипеда (см. рис. 43).
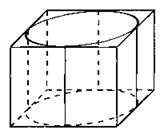
Рис. 43.
В12. Независимое агентство намерено ввести рейтинг R новостных изданий на основе показателей информативности In, оперативности Ор и объективности Тr публикаций. Каждый показатель оценивается целыми числами от —3 до 3. Аналитик, составляющий формулу, считает, что объективность публикаций ценится вдвое, а информативность — вчетверо дороже, чем оперативность. В результате формула примет вид ![]() Каким должно быть число А, чтобы издание, у которого все показатели наибольшие, получило рейтинг 105?
Каким должно быть число А, чтобы издание, у которого все показатели наибольшие, получило рейтинг 105?
В13. Первые 360 км автомобиль ехал со скоростью 60 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 200 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В14. Найдите наименьшее значение функции у = х3 — 4х2 — 3х + 2 на отрезке [2; 5].
Часть 2
С1. а) Решите уравнение 33 cos x ∙ cos 2x = 1/3.
б) Найдите все корни этого уравнения, принадлежащие промежутку ![]()
С2. В прямоугольном параллелепипеде ABCDA1B1C1D1 точка К — середина ребра BB1, A1B1C1D1 — квадрат, В1К = 3, а синус угла между плоскостями ABD и АКС равен 3/4. Найдите ВС.
С3. Решите систему неравенств
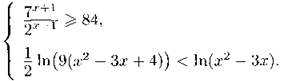
С4. На стороне АВ и CD прямоугольника ABCD взяты соответственно точки К и М так, что в трапеции МКВС и AKMD можно вписать круги, площадь каждого из которых в 4 раза меньше площади ABCD. Прямые, содержащие отрезки МК и ВС, пересекаются в точке Р. Найдите расстояние от точки Р до АВ, если точка М делит сторону CD в отношении 3 : 7, АВ = 10.
С5. При каких значениях параметра а система ![]() имеет более двух решений?
имеет более двух решений?
С6. Через n! обозначается произведение натуральных чисел от 1 до n. Например, 6! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720. Для любого натурального числа k будем через d(k) обозначать количество его делителей, включая 1 и само число k. Могут ли выполняться следующие равенства? Если да, то для каких n они выполняются?
a) d((n!)2) = 18281828
б) d((n!)2) = 105
в) d(2n(n!)2) = 108