Вариант № 3 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Поезд Москва — Нижний Новгород отправляется в 21 : 40, а прибывает в 5 : 10 на следующий день (время московское). Сколько часов поезд находится в пути?

В2. На рисунке 31 точками показана среднесуточная скорость ветра с 20 января по 7 февраля 2011 года. По горизонтали указываются числа месяца, по вертикали — скорость ветра в м/с. Для наглядности точки на рисунке соединены линиями. Определите по рисунку наибольшую среднесуточную скорость ветра (в м/с) за указанный период.

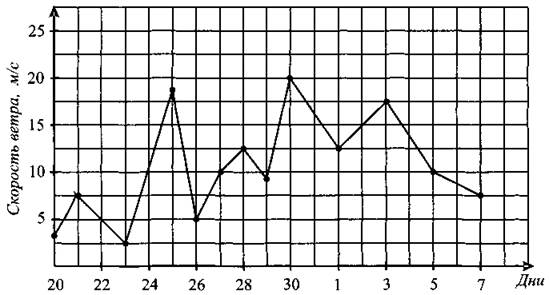
Рис. 31.

В3. Найдите площадь трапеции, вершины которой имеют координаты (1; 1), (1; 4), (10; 0), (10; 7) (см. рис. 32).

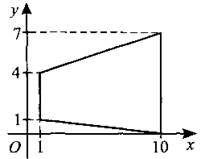
Рис. 32.

В4. Автомобильный журнал определяет рейтинги автомобилей на основе показателей безопасности S, комфорта С, функциональности F, качества Q и дизайна D. Каждый отдельный показатель оценивается по 5-балльной шкале. Рейтинг R вычисляется по формуле

Модель	Безопасность	Комфорт	Функциональность	Качество	Дизайн
А	3	2	5	2	1
Б	4	3	4	1	3
В	5	1	3	3	1

В таблице даны оценки каждого показателя для трёх моделей автомобилей. Определите наивысший рейтинг среди представленных в таблице моделей автомобилей.

В5. Найдите корень уравнения

В6. В треугольнике ABC BD — биссектриса (см. рис. 33). Угол А равен 94°, угол ABD равен 7°. Найдите градусную меру угла С.

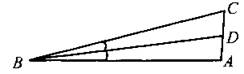
Рис. 33.

В7. Найдите значение выражения (2x⁴)² : 2х⁸ при х = 0,85.

В8. Материальная точка движется прямолинейно по закону x(t) = 21³ + t² — 5t, где х — расстояние от точки отсчёта в метрах, t — время в секундах, измеряемое с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 4 с.

В9. Площадь боковой поверхности цилиндра равна 27л, а диаметр основания равен 6. Найдите высоту цилиндра.

В10. В чемпионате мира участвуют 24 команды, в том числе команда России. С помощью жребия их нужно разделить на четыре группы по шесть команд в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4.

Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в третьей группе?

В11. Цилиндр и конус имеют общее основание и общую высоту (см. рис. 34). Вычислите объём конуса, если объём цилиндра равен 60.

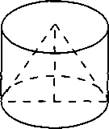
Рис. 34.

В12. Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома I = U/R, где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включён предохранитель, который плавится, если сила тока превышает 15 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 240 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.

В13. Куртка стоила 3200 рублей. В январе её цена снизилась на 4%, а в феврале поднялась на 25% от январской цены. Сколько рублей стала стоить куртка?

В14. Найдите наибольшее значение функции у = 15х² — х³ на отрезке [—1; 10].

Часть 2

С1. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

С2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны рёбра АВ = 10, AD = 11, ВВ₁ = 7. Точка К принадлежит ребру СС₁ и делит его в отношении 2 : 5, считая от вершины С. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки В, К и D₁.

С3. Решите систему неравенств

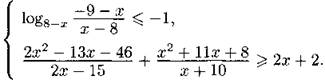
С4. Окружности радиусов 22 и 42 с центрами O₁ и О₂ соответственно касаются внутренним образом в точке Р, КО₁ и LO₂ — параллельные радиусы этих окружностей, причём ∠KO₁O₂ = 120°. Найдите KL.

С5. Найдите все значения параметра а, при каждом из которых уравнение имеет единственный корень.

С6. Задумано несколько целых чисел. Набор этих чисел и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Например, если задуманы числа —4, 8, 12, то на доске будет выписан набор -4, 4, 8, 8, 12, 16, 20.

а) На доске выписан набор —5, —3, —2, 2, 4, 5, 7. Какие числа были задуманы?

б) Для некоторых различных задуманных чисел в наборе, выписанном на доске, число 0 встречается ровно 2 раза. Какое наименьшее количество чисел могло быть задумано?

в) Для некоторых задуманных чисел на доске выписан набор. Всегда ли по этому набору можно однозначно определить задуманные числа?