Вариант № 1 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Теплоход рассчитан на 860 пассажиров и 33 члена команды. Каждая спасательная шлюпка может вместить 60 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?

В2. На рисунке 20 точками показана цена акций компании «Газпром» на момент закрытия биржевых торгов во все рабочие дни января 2011 года. По горизонтали указываются числа месяца, по вертикали — цена акции в рублях. Для наглядности точки на рисунке соединены линией. Определите по рисунку, какого числа рассматриваемого периода цена акций «Газпрома» на момент закрытия торгов была наименьшей.

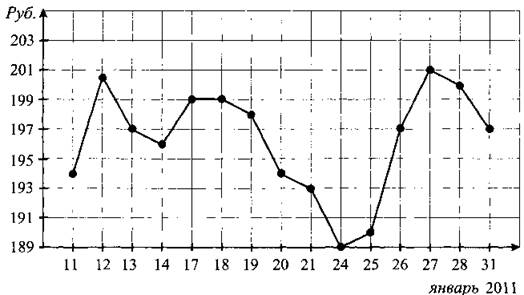
Рис. 20.

В3. Найдите площадь треугольника, вершины которого имеют координаты (1; 4), (4; 10), (6; 4) (см рис. 21).

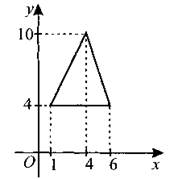
Рис. 21.

В4. Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана:

Тарифный план	Абонентская плата	Плата за трафик
1. «Вера»	2000 рублей за 1000 Mb трафика в месяц	5 рублей за каждый Mb сверх 1000 Mb
2. «Надежда»	600 рублей за 400 Mb трафика в месяц	3 рубля за каждый Mb сверх 400 Mb
3. «Любовь»	50 рублей за 150 Mb трафика в месяц	2,5 рубля за каждый Mb сверх 150 Mb

Абонент предполагает, что его трафик составит 1100 Mb. Сколько рублей заплатит он по наиболее выгодному тарифному плану, если его предположение окажется верным?

В5. Найдите корень уравнения 11^x-10 = 11.

В6. В трапеции ABCD (см. рис. 22). Найдите косинус угла В.

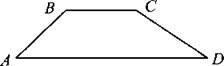
Рис. 22.

В7. Найдите значение выражения log₂ 1,6 + log₂ 10.

В8. На рисунке 23 изображён график функции у = f(x) и отмечены десять точек на оси абсцисс: x₁, x₂, x₃, ..., x₁₀. В скольких из этих точек производная функции f(x) положительна?

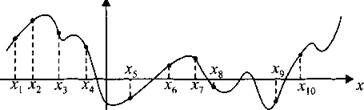
Рис. 23.

В9. Основанием прямой треугольной призмы (см. рис. 24) служит прямоугольный треугольник с катетами 9 и 12, высота призмы равна 10. Найдите площадь её поверхности.

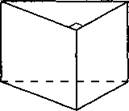
Рис. 24.

В10. На конференцию приехали 7 учёных из Германии, 8 из России и 5 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что третьим окажется доклад учёного из России.

В11. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 5 (см. рис. 25). Найдите объём параллелепипеда.

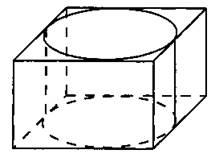
Рис. 25.

В12. Зависимость объёма спроса q на продукцию предприятия-монополиста от цены р задаётся формулой q = 300 — 60р. Месячная выручка r определяется как r(p) = q ∙ р (тыс. руб.). Определите максимальный уровень цены р (тыс. руб.), при котором величина месячной выручки предприятия составит не менее 315 тыс. руб.

В13. Из городов АиВ, расстояние между которыми 270 км, одновременно навстречу друг другу выехали два автобуса, которые встретились на расстоянии 140 км от А. Найдите скорость автобуса (в км/час), выехавшего из пункта В, если автобусы встретились через 2,5 часа.

В14. Найдите точку максимума функции у = (10 — х)е^х+10.

Часть 2

С1. а) Решите уравнение 12^{sin x} = 3^{sin x} ∙ 4^{cos x}.

б) Найдите все корни этого уравнения, принадлежащие отрезку .

С2. В правильной четырёхугольной пирамиде SABCD с вершиной в точке S стороны основания равны 12, а боковые рёбра равны 24. Найдите площадь сечения пирамиды плоскостью, проходящей через точку D и середину ребра SB параллельно прямой АС.

С3. Решите систему неравенств

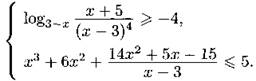
С4. Окружности радиусов 4 и 6 с центрами O₁ и O₂ соответственно касаются в точке К. Прямая, проходящая через точку К, вторично пересекает меньшую окружность в точке М, а большую в точке N. Найдите площадь треугольника MNO₂, если ∠КМО₁ = 15°.

С5. Найдите все значения а, при каждом из которых уравнение имеет единственный корень.

С6. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-нибудь число k, выписанное на доску, повторяется несколько раз, то на доске остаётся одно такое число k, а остальные числа, равные k, стираются. Например, если задуманы числа 2, 3, 5, 7, то на доске будет записан набор 2, 3, 5, 7, 8, 9, 10, 12, 14, 15, 17.

а) Приведите пример задуманных чисел, для которых на доске будет записан набор 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.

б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 2, 3, 5, 7, 8, 9, 12, 15, 17, 18, 20, 21, 22, 25?

в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 9, 13, 16, 20, 22, 26, 29, 33, 35, 39, 42, 46, 48, 55?