Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Геометрические задачи в пространстве
3.1. На луче, перпендикулярном к MN, возьмем произвольную точку А (рис. P.3.1). Спроецируем OA на плоскость P, а полученный отрезок OB на второй из данных лучей. Треугольник АСО прямоугольный (по теореме о трех перпендикулярах).
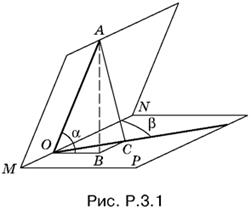
Косинус искомого угла АОС равен ОС/OA. Используя построенным треугольники, можно выразить ОС через OA:
ОС = OB sin β = OA cos α sin β.
Ответ. arccos (cos α sin β).
3.2. Спроецируем данный треугольник ABC на плоскость P (рис. P.3.2) и построим угол CED, равный x, между плоскостью треугольника и плоскостью P. Введем в рассмотрение линейный элемент CD = а.
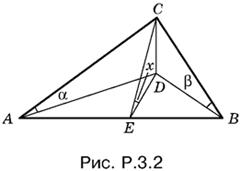
Тогда
![]()
Так как СЕ — высота в треугольнике ABC, опущенная на гипотенузу, то (из сравнения площадей) имеем
![]()
Подставляя вычисленные раньше значения AC, BC и СЕ, получим
![]()
откуда
![]()
Так как угол x по построению всегда острый, то он определяется однозначно.
Ответ.
![]()
3.3. Из некоторой точки В1 на стороне угла α опустим перпендикуляр B1B на плоскость P (рис. P.3.3). Через В1 проведем плоскость, параллельную плоскости P. Она пересечет другую сторону угла α в некоторой точке А1. Через B1B и А проведем плоскость, которая будет перпендикулярна к плоскости P.
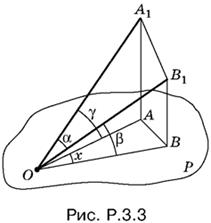
Отрезки AA1 и ВВ1 равны. Обозначим АА1 = ВВ1 = а. Теперь можно вычислить все стороны треугольника ОАВ и воспользоваться теоремой косинусов, чтобы найти угол x.
Стороны OA и OB вычислить просто:
OA = а ctg γ, OB = а ctg β.
Сторона AB равна А1В1 в треугольнике ОА1В1. Так как
![]()
то по теореме косинусов
![]()
Воспользуемся теоремой косинусов еще раз, но уже для треугольника ОАВ:
АВ² = ОА² + ОВ² − 2ОА · OB cos x.
Подставляя сюда найденные выше выражения для OA, OB и AB, получим уравнение относительно cos x. Решая его, после несложных тригонометрических преобразований найдем cos x.
Ответ.
![]()
3.4. Построим плоскость P, перпендикулярную к прямой а, и спроецируем на нее прямые b, с и d. Искомая прямая параллельна а, т. е. должна спроецироваться в точку О на плоскости P. Точка О будет одинаково удалена от проекций b1, с1 и d1 трех этих прямых.
Поскольку прямые а, b, с и d скрещивающиеся, ни одна из прямых b, с и d не может спроецироваться в точку на плоскости P, так как иначе она оказалась бы параллельной прямой а.
Проекции никаких двух прямых из b, с, d не сольются, так как это означало бы, что эти две прямые лежат в одной плоскости. Поэтому проекции b1, с1 и d1 могут расположиться на плоскости P лишь одним из четырех способов (рис. P.3.4, а).
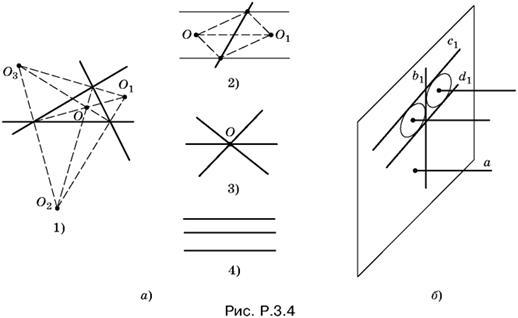
B первом случае (проекции образуют треугольник) мы получим четыре точки, равноотстоящие от b1, с1 и d1. Это — центры вписанной и вневписанных окружностей. Проводя через каждую из них прямую, перпендикулярную к плоскости P, придем к четырем решениям.
Во втором случае (две из проекций параллельны) получим два решения (рис. P.3.4, б).
B третьем случае (проекции пересекаются в одной точке) будет единственное решение — прямая, проходящая через общую для трех проекций точку.
B последнем случае (проекции b1, с1 и d1 параллельны) решения нет.
Так как все возможные случаи исчерпаны, то задача решена.
3.5. Проведем CD параллельно AB (рис. P.3.5).
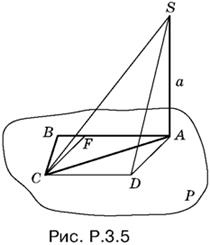
Угол SCD искомый. Построим CF ⊥ AB и AD ⊥ AB. B прямоугольнике AFCD имеем CD = АF = а/2, AD = CF = . Из треугольника SAD находим
![]()
Тангенс угла SCD равен SD : CD.
Ответ. √7.
3.6. Если OK = ½AB = OA, то треугольники OAM и OKM (рис. P.3.6) равны. Таким образом, условие OK = OA равносильно условию AM = KM и (совершенно аналогично) условию BP = KP.
Отрезок OK входит в оба треугольника OKM и OKP:
OK² = OM² − m², OK² = OP² − l², т. е. OM² − m² = OP² − l²
(через m и l обозначены длины отрезков MK и KP соответственно).
Так как OM² = а² + AO², а OP² = b² + OB² и AO = OB, то
а² − m² = b² − l²
или
m² − l² = а² − b². (1)
Точно так же приравняем выражения для отрезка AP², полученные из треугольников MAP и ABP:
(m + l)² − а² = b² + AB².
Вспомнив, что по условию AB² = 2ab, получим (m + l)² = а² + 2ab + b², т. е.
m + l = а + b. (2)
Разделив почленно равенство (1) на равенство (2), получим
m − l = а − b, (3)
а решая систему из уравнений (2) и (3), найдем m = а, b = l, что и требовалось доказать.
3.7. Обозначим через PQ (рис. P.3.7) прямую, по которой пересекаются грани AOD и BOC, а через RS — прямую, по которой пересекаются грани AOB и DOC. Прямые PQ и RS определяют плоскость P. Через произвольную точку M на АО проведем плоскость, параллельную плоскости P. Фигура MNKL, получившаяся в сечении, будет параллелограммом.
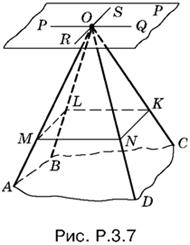
B самом деле, MN || PQ и LK || PQ, a ML || RS и NK || RS, как прямые, получившиеся в результате пересечения двух параллельных плоскостей третьей. Следовательно, MN || LK и ML || NK, что и требовалось доказать.
3.8. Продолжим ED и CB (рис. P.3.8) до пересечения в точке F и проведем AF — ребро двугранного угла, косинус которого нужно найти.
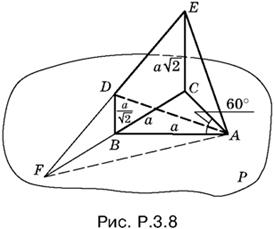
Так как EC = 2DB (по условию), то DB — средняя линия в треугольнике EFC. Поэтому FB = BC = а. Поскольку BA = а, то треугольник FBA равнобедренный. Сумма его углов, прилежавших к FA, равна 60°, а угол BAF равен 30°.
Мы убедились в том, что угол CAF прямой, а следовательно, линейный угол EAC измеряет искомый двугранный угол. Теперь остаются простые вычисления:
![]()
По теореме о трех перпендикулярах отрезки EA и FA взаимно перпендикулярны; поэтому площадь треугольника EAF равна ½EA · AF, где AF = а√3 . Итак, площадь треугольника AFE равна 3a²/2, и вследствие того, что FD = DE, площадь треугольника DEA в два раза меньше.
Ответ. 3a²/2, 1/√3.
3.9. Обозначим высоту SO пирамиды через H. Предположим, что вершина пирамиды спроецируется в точку O, лежащую внутри треугольника ABC, и пусть углы SDO, SEO и SFO измеряют данные двугранные углы (рис. P.3.9, а).
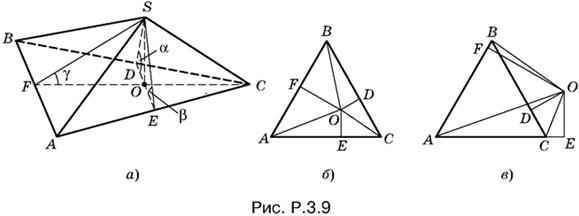
Рассмотрим отдельно треугольник ABC (рис. P.3.9, б). Площадь его, с одной стороны, равна сумме площадей треугольников AOB, BOC и COA, а с другой стороны, равна a²√3/4. Поэтому
½a(OF + OD + OE) = a²√3/4, т.е. OF + OD + OE = a√3/2.
Каждый из отрезков OF, OD и OE можно выразить через H:
OD = H ctg α, OE = H ctg β, OF = H ctg γ. Следовательно,
H = a√3/2(ctg α + ctg β + ctg γ).
Если точка О лежит вне треугольника ABC, то один из данных двугранных углов тупой (на рис. P.3.9, в угол при BC, т. е. α). Следовательно, его котангенс будет отрицательным. Это соответствует тому факту, что площадь треугольника ABC равна сумме площадей треугольников АВО и АОС за вычетом площади треугольника ВОС. Таким образом, результат останется таким же, как в случае, когда О лежит внутри треугольника ABC.
Наконец, как легко убедиться, полученная формула дает верный результат и в том случае, когда точка О лежит на стороне треугольника ABC или совпадает с его вершиной. (Соответствующие котангенсы обращаются в нуль.)
Ответ. V = a³/8(ctg α + ctg β + ctg γ).
3.10. Так как AC = BC по условию (рис. P.3.10), то прямоугольные треугольники ADC и BDC равны и, следовательно, AD = BD. Треугольник ADB — равнобедренный, его медиана DE, проведенная из вершины D, будет одновременно и высотой. Таким образом, мы доказали, что двугранный угол при ребре AB измеряется линейным углом DEC, который обозначим через x.
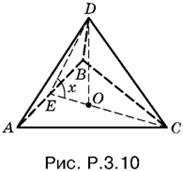
Высота DO треугольника EDC будет высотой пирамиды. B самом деле, ребро AB перпендикулярно к ED и EP, т. е. к плоскости EDC. Отрезок DO, следовательно, перпендикулярен не только к EC, но и к AB, т. е. перпендикулярен к плоскости ABC.
Заметим также, что CD — перпендикуляр к плоскости ADB, а поэтому треугольник EDC прямоугольный с прямым углом при вершине D.
Мы знаем, что V = ⅓S · OD. Отрезок OD равен ED sin x, а отрезок ED в свою очередь равен EC cos x, т. е. 2S/a cos x.
Итак,
V = ⅓S · 2S/a cos x sin x,
откуда sin 2x = 3Va/S².
Чтобы найти x, заметим, что угол x острый.
Ответ. ½acrsin 3aV/S².
3.11. Так как площадь основания равна √3, то сторона основания равна 2. Из треугольника AOS (рис. P.3.11) находим AO = b cos x; с другой стороны,
AO = ⅔AD = ⅔ a√3/2.
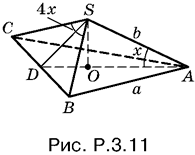
Поэтому
a/√3 = b cos x.
Из треугольника CDS находим CD = a/2 = b sin 2x. Разделив второе соотношение на первое, получим
sin x = √3/4.
Так как SD = a/2 ctg 2x, то нужно вычислить ctg 2x:
![]()
Следовательно, SD = 5/√39, а площадь боковой поверхности равна 3/2а · SD.
Ответ. 5/√39.
3.12. На рис. P.3.12 треугольники AEC и С1ЕА1 подобны, так как медианы AE и СЕ делятся точками C1 и A1 в одинаковом отношении 2:1.
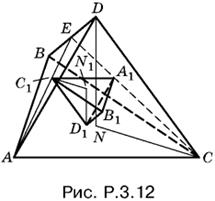
Поэтому C1A1 = ⅓ AC. Аналогично доказывается, что В1А1 = ⅓ AB и C1B1 = ⅓ BC и т. д., т. е. площади S1 и S оснований пирамиды относятся как 1 : 9. Подобные треугольники ABC и A1B1C1 лежат в параллельных плоскостях, так как их стороны параллельны. Следовательно, высоты DN и D1N1, проведенные в тетраэдрах, параллельны и прямоугольные треугольники DNC и D1N1C1 подобны, т. е. D1N1 = ⅓ DN. Остается сравнить объемы
![]()
Ответ. 1/27.
3.13. Пусть О1, О2 и О3 — точки пересечения медиан соответствующих граней (на рис. P.3.13 изображены лишь О1 и О2), О — центр шара.
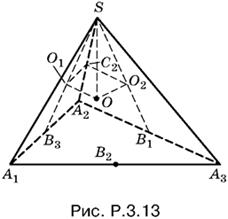
Прямоугольные треугольники SO1О, SO2О и SO3О равны (О1О = О2О = О3О, OS — общая гипотенуза). Следовательно, SO1 = SO2 = SO3, и поэтому SB1 = SB2 = SB3.
Докажем теперь, что треугольник А1А2А3 правильный. Для этого достаточно установить равенство треугольников A2SB1 и A2SB3, т. е. любых соседних из шести таких треугольников. Установим в них равенство углов при вершине S. Пусть C2 — точка пересечения плоскости О1ОО2 с ребром SA2. Прямоугольные треугольники О1SC2 и О2SC2 тоже равны. Отсюда углы О1SC2 и О2SC2 равны и, следовательно, равны треугольники B1SA2 и B3SA2. Таким образом, В1А2 = В3А2, т. е. А2А3 = А1А2. Итак, в основании пирамиды лежит правильный треугольник.
Из равенства треугольников B1SA2 и B3SA2 следует также равенство треугольников A1SA2 и A2SA3, т. е. равенство всех боковых ребер. Это означает, что вершина S проецируется в центр основания А1А2А3. Тем самым доказано, что пирамида правильная.
3.14. Достроим пирамиду до полной. Все параллельные сечения пирамиды подобны. Составим схематический рис. P.3.14, на котором А и B — стороны квадратов, равновеликих основаниям, M — сторона квадрата, равновеликого сечению, проходящему через середину высоты данной усеченной пирамиды. Последнее условие мы запишем так:
![]()
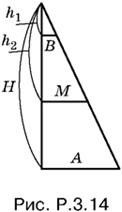
Из подобия треугольников, изображенных на рис. P.3.14, следует, что
![]()
откуда
![]()
Составим среднее арифметическое величин А и B:
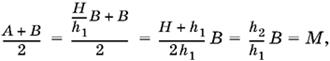
что и требовалось доказать.
3.15. Достроим треугольник ABC до параллелограмма ABCE (рис. P.3.15). Угол DAE равен углу между AD и BC. Обозначим его через x.
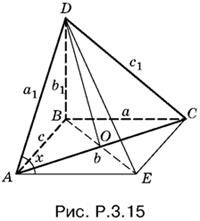
B треугольнике DAE
AD = а1, AE = а.
Вычислим DE. Так как в дальнейшем мы воспользуемся теоремой косинусов, то удобнее находить DE².
Отрезок DO является медианой в треугольниках ADC и BDE:
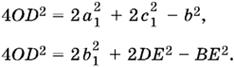
Чтобы найти DE², достаточно вычислить BE². Но ВЕ — диагональ параллелограмма ABCЕ, т. е. ВЕ² = 2а² + 2с² − b². Следовательно,
![]()
Применим к треугольнику ADE теорему косинусов:
DE² = a1² + a² − 2aa1 cos x.
Приравнивая два выражения для DЕ², найдем cos x. При этом следует иметь в виду, что по определению угла между скрещивающимися прямыми x — острый угол.
Ответ.
![]()
3.16. Плоскость ABE (рис. P.3.16) делит тетраэдр на две пирамиды SABE и CABE с общим основанием ABE.
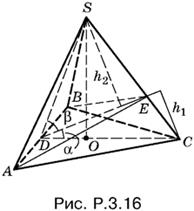
Так как отношение объемов дано, а основание у пирамиды общее, то h2 : h1 = 5 : 3, в силу же равенства SD = CD имеем
sin α/sin β = 3/5, т.е. sin α = 3/5 sin β.
Кроме того, так как тетраэдр правильный, углы α и β образуют угол SDO, косинус которого равен 1. Поэтому
cos α cos β − sin α sin β = ⅓.
Выразив в этом уравнении sin β и cos β через sin α (так как пирамида правильная, углы α и β острые), получим
![]()
где y = sin² α.
Возведем в квадрат и раскроем скобки; найдем y = 2/11 и вычислим tg α:
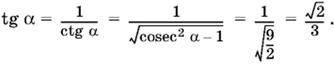
Поскольку sin² β = 25/9 sin² α = 50/99, то аналогично найдем tg β.
Ответ. 5√2/7, √2/3.
3.17. Треугольники DAM и DMS (рис. P.3.17) имеют общую высоту, проведенную из вершины D. Поэтому отношение их площадей равно отношению оснований AM и MS.
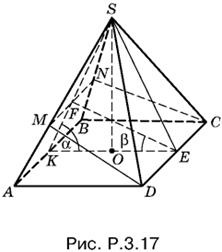
Из подобия треугольников MSF и ASK следует, что AM : MS = KF : FS.
Отрезки KF и FS выразим через KE. По теореме синусов для треугольника KFE имеем
KF = KE sin β/sin (α + β).
Так как KS = KE/2 cos α, то
FS = KS − KF = KE/2 cos α − KE sin β/sin (α + β) = KE sin (α − β)/2 cos α sin (α + β)
(впрочем, это можно установить и непосредственно из треугольника EFS).
Остается найти отношение KF : FS.
Ответ. 2 sin β cos α/sin (α − β).
3.18. По условию высоты DO пирамиды проходит через точку пересечения высот основания. Поэтому, соединив точку О с вершиной С и продолжив до пересечения с AB, получим отрезок СЕ, являющийся высотой треугольника ABC, опущенной на сторону AB (рис. P.3.18).
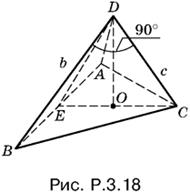
Прямая AB перпендикулярна к DO и EC, следовательно, прямые AB и CD тоже перпендикулярны друг другу. Таким образом, прямая CD перпендикулярна к двум прямым BD и AB плоскости ABD, а потому перпендикулярна к прямой AD. Мы доказали, что угол ADC прямой. Аналогично доказывается, что прямые BD и AD тоже перпендикулярны.
Теперь нетрудно ответить на вопрос задачи: площадь треугольника ADB равна ½b · AD, а площадь треугольника ADC равна ½с · AD. Отношение площадей равно отношению неравных катетов.
Ответ. b/c.
3.19. Объем пирамиды SABC (рис. P.3.19) равен удвоенному объему пирамиды с основанием DSC и высотой AD.
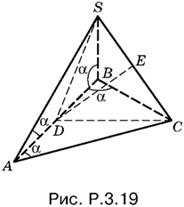
Так как AD = a/2, то этот объем равен Sa/6, а объем всей пирамиды равен Sa/3, где через S обозначена площадь SDC.
Проведем высоту DE и вычислим EC и DE.
Треугольник CAS равнобедренный (AS = AC), поэтому
EC = AC sin α/2 = a/2 cos α sin α/2.
Так как DC = a/2 tg α, то
Остается вычислить объем:
V = aS/3 = a/3 · DE · EC.
Ответ.
![]()
3.20. Рассмотрим два случая:
α ≤ π/2, α > π/2.
Если угол α не тупой, то (рис. P.3.20, a) CD = SD = AB/2.
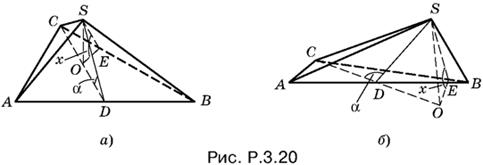
Пусть SO — высота пирамиды, SD и SE — высоты в треугольниках ASB и CSB. Из треугольника SOD
OS = SD sin α = AB/2 sin α, OD = AB/2 cos α.
B треугольнике COE угол OEC прямой, а угол OCE равен 45°. Поэтому
OE = OC/√2 = 1/√2(CD − OD) = AB/2√2(1 − cos α).
Теперь можно найти тангенс искомого угла:
tg x = OS/OE = √2 ctg α/2.
Если угол α тупой, то (рис. P.3.20, б) снова получим CD = SD = AB/2. Высота OS равна
OS = SD sin (π − α) = AB/2 sin α,
отрезок OD равен
OD = SD cos (π − α) = − AB/2 cos α
(угол α тупой и cos α < 0). Треугольник СОЕ тоже прямоугольный и равнобедренный. Поэтому
OE = CO/√2 = 1/√2(CD + OD) = AB/2√2(1 − cos α).
Так как для OE и OS получились такие же значения, как в первом случае, то и окончательный результат не изменится.
Ответ. x = arctg (√2 ctg α/2).
3.21. Проведем в треугольнике ABC (рис. P.3.21) высоту BD и соединим точку D с вершиной S пирамиды. Так как ребро SB образует равные углы с ребрами SC и SA, то SD — биссектриса угла ASC.
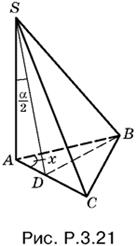
Рассмотрим прямоугольный треугольник ABD. B нем
AD = SA · tg α/4, AB = SA · tg α, т. е.
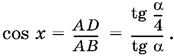
Так как α — угол прямоугольного треугольника, то 0 < α < π/2, а потому tg α/4 < tg α и правая часть уравнения меньше единицы.
Ответ.

3.22. Пусть M — середина AB. Тогда медианы СМ и DM (рис. P.3.22) являются одновременно высотами в равнобедренных треугольниках ABC и ABD. Следовательно, прямая AB перпендикулярна к плоскости CMD, а потому и к прямой CD, лежащей в этой плоскости. Треугольник CMD равнобедренный, так как СМ и MD — медианы, проведенные к общей стороне в равных треугольниках. Следовательно, его высота MK будет одновременно и медианой. Итак, отрезок KM, соединяющий середины AB и CD, есть общий перпендикуляр к этим ребрам. Поэтому центр описанного около тетраэдра ABCD шара должен лежать на этом отрезке.
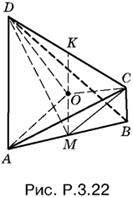
Из треугольников MDB и MDK последовательно находим MD = √65, MK = 7. С другой стороны, из треугольников OKD и AMO находим
![]()
Получаем уравнение
![]()
Ответ. R = 5.
3.23. Проведем через точку O (рис. P.3.23) сечение B1EC1 пирамиды, перпендикулярное к стороне SA. Тогда угол B1EC1 равен α, а OE = а. Так как пирамида правильная, то в силу симметрии треугольник B1EC1 равнобедренный, а B1C1 и BC параллельны.
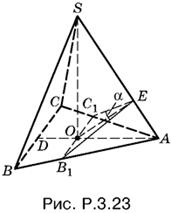
Чтобы связать высоту SO с элементами треугольника B1EC1, рассмотрим треугольник SOA, для которого воспользуемся сравнением площадей:
SO · OA = OE · SA. (4)
Выразим все участвующие в этом соотношении отрезки через а, α и h:
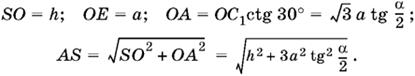
Подставив в уравнение (4) и возведя затем обе части уравнения в квадрат, получим уравнение
3h² tg² α/2 − h² = 3a² tg² α/2,
откуда
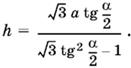
Чтобы привести это выражение к виду, удобному для логарифмирования, преобразуем выражение, стоящее в знаменателе под радикалом:
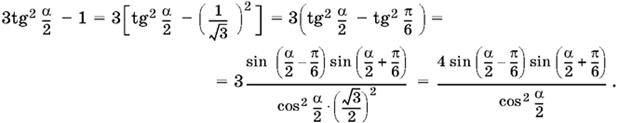
Ответ.
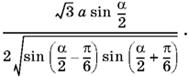
3.24. Если в сечении образуется квадрат, то плоскость сечения пересекает все четыре грани пирамиды. Кроме того, отрезок KL параллелен MN, т. е. параллелен плоскости основания, а следовательно, и ребру AB.
Аналогично отрезки KM и LN параллельны ребру DC. Итак, если в сечении пирамиды — квадрат, то плоскость сечения должна быть параллельной двум скрещивающимся прямым, на которых лежат ребра AB и DC.
Докажем обратное: если провести сечение пирамиды, плоскость которого параллельна AB и DC, то в сечении получится прямоугольник. B самом деле, то, что это будет параллелограмм, устанавливается непосредственно. Спроецировав DC на плоскость основания (рис. P.3.24), мы убедимся в том, что MN и EC взаимно перпендикулярны. Отсюда следует, что прямым будет угол между DC и MN, а значит, и между LN и MN. Таким образом, KLMN — прямоугольник.
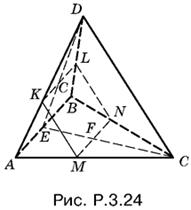
Мы доказали, что в сечении можно получить прямоугольник только с помощью плоскости, параллельной двум скрещивающимся ребрам.
Этот прямоугольник будет квадратом, если MN = MK. Из подобия треугольников ADC и AMK находим MK/CD = AM/AC, причем
![]()
Подставляя в первоначальное отношение, получим
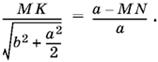
Так как MK = MN, то получим уравнение относительно стороны квадрата, из которого
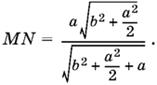
Ответ.
![]()
3.25. Расположим пирамиду так, как показано на рис. P.3.25.
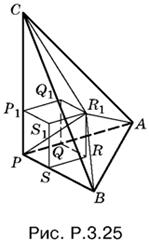
Соединим вершину R1 куба с вершинами пирамиды. Пирамида АBCР разобьется на три пирамиды: R1ABP, R1ACP, R1BCP, y которых общая вершина R1 и одинаковая высота x, равная по длине ребру куба. Из сравнения объемов получим
1/6abc = 1/6(xab + xbc + xac),
откуда найдем x.
Ответ. abc/ab + bc + ac.
3.26. Верхнее основание куба будет вписано в равносторонний треугольник A1B1C1 (рис. P.3.26) подобный основанию ABC пирамиды.
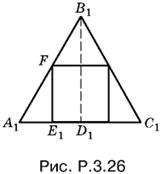
Выразим сторону A1C1 треугольника A1B1C1 через сторону вписанного квадрата:
A1C1 = 2A1E1 + a = 2a ctg 60° + a = a(1 + 2/√3).
Площадь треугольника A1B1C1 тогда равна
![]()
Так как треугольники ABC и A1B1C1 подобны и расстояние первого от центра подобия равно h, а расстояние второго равно h − а, то отношение площадей равно h²/(h − a)². Поэтому площадь треугольника ABC равна
![]()
Ответ.
![]()
3.27. Пусть трехгранный угол пересечен некоторой плоскостью и в сечении образовался треугольник со сторонами a, b и с (рис. P.3.27).
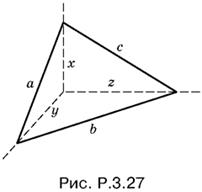
Обозначим через x, y и z боковые ребра образовавшейся пирамиды, если ее вершиной считать вершину данного трехгранного угла. Тогда объем этой пирамиды равен xyz/6. Поскольку все плоские углы, образующие трехгранный угол, прямые, имеем
x² + y² = a², y² + z² = b², z² + x² = с².
Сложим эти уравнения, найдем x² + y² + z² = ½(а² + b² + с²). Теперь легко определить x, y и z. Таким образом,
![]()
Если треугольник в сечении тупоугольный и а ≤ b < с, то а² + b² < с², т. е. первая скобка под корнем отрицательна, в то время как остальные положительны. Если же треугольник в сечении прямоугольный, то одна из скобок обращается в нуль. Таким образом, нет сечения трехгранного угла, которое не было бы остроугольным треугольником.
3.28. Осуществив построения, изображенные на рис. P.3.28, постараемся вычислить объем данной пирамиды как удвоенный объем пирамиды AODC с вершиной в точке A (равенство объемов AODC и BODC станет очевидным из дальнейшего). Докажем вначале, что AFBE — прямоугольник. Из равенства треугольников CFB и DEA следует, что EA = BF. Аналогично BE = FA. Следовательно, AFBE — параллелограмм. Но EF = AB, а потому эта фигура — прямоугольник. Чтобы найти площадь треугольника DOC, нужно вычислить его высоту CF, для чего достаточно знать стороны прямоугольника AFBE.
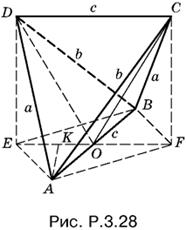
Отрезок CF может быть найден из двух прилегающих к нему прямо угольных треугольников. С одной стороны, CF² = BC² − BF², с другой стороны, CF² = AC² − AF², т. е. BF² − AF² = а²− b².
Составим систему уравнений:
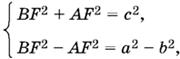
из которой найдем BF² = ½(а² − b² + с²), AF² = ½(с² − а² + b²). Теперь можно вычислить CF и AK:
CF² = а² − ½(а² − b² + с²) = ½(а² + b² + с²),
![]()
Объем пирамиды ABCD равен 2 · ⅓AK(½DC · CF).
Ответ.
![]()
3.29. Расположим пирамиду ABCD так, как показано на рис. P.3.29, а. Воспользуемся методом сравнения объемов по отношению к телу ANBMCD.
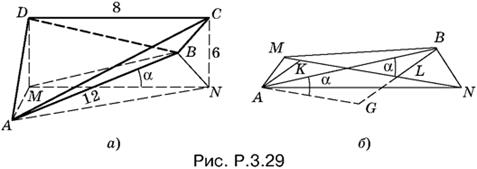
С одной стороны, его можно рассматривать как составленное из двух пирамид с общим основанием MNCD и с вершинами в точках A и B. Основание MNCD — прямоугольник с известными сторонами. Высотами будут перпендикуляры AK и BL, опущенные на MN (рис. P.3.29, б). Так как нам нужна сумма объемов двух пирамид с общим основанием, то выразим AK + BL через AB и sin α. Тогда объем нашего тела будет выражен через α.
С другой стороны, VANBMCD = VABCD + VABMD + VABNC.
Проведем AG || KL (см. рис. P.3.29, б). Тогда
AK + BL = GB = 12 sin α, SMNCD = 6 · 8 = 48,
VANBMCD = ⅓ SMNCD(AK + BL) = 4 · 48 sin α,
SMANB = ½ AB · NM sin α = 48 sin α.
VABCD + VABMD + VABNC = 48 + 6/3(SABM + SABN) = 48 + 2SMANB = 48 + 2 · 48 sin α.
Таким образом,
48 + 2 · 48 sin α = 4 · 48 sin α.
Отсюда
sin α = ½.
Ответ. α = π/6.
3.30. Поставим четырехугольную пирамиду A1BB1C1C, в которую вписан шар, на основание BB1C1C (рис. P.3.30). Пусть H — высота призмы, а — сторона ее основания. Радиусы окружностей с центрами O и O1 равны R. Так как треугольник B1A1C1 правильный, то а = 2√3 R.
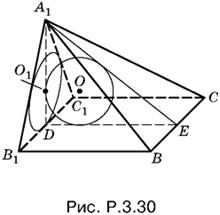
Рассмотрим треугольник DA1E. Он прямоугольный и его площадь, с одной стороны, равна ½A1D · DE, а с другой стороны, R/2(A1D + DE + A1E). Поскольку
![]()
получаем уравнение относительно H, которое после подстановки а = 2√3 R и возведения в квадрат принимает вид H² = 4HR, откуда H = 4R.
Ответ. 12√3 R³.
3.31. Центр шара, касающегося трех ребер правильного тетраэдра, исходящих из общей вершины, должен лежать на биссектрисе соответствующего трехгранного угла, которая совпадает с высотой тетраэдра, опущенной из этой же вершины. Поскольку все четыре биссектрисы пересекаются в одной точке — центре вписанного в тетраэдр шара, достаточно рассмотреть треугольник SOA (рис. P.3.31), где SO — высота тетраэдра, SA — его ребро, а O1 — центр искомого шара и шара, вписанного в тетраэдр.
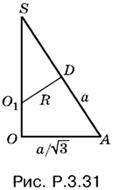
Треугольники SAO и SO1D подобны. B первом известны все стороны, во втором SO1 = a√6/4. = . Это позволяет вычислить R.
Ответ. a√2/4.
3.32. Если один куб расположен внутри другого, а вершина O y них общая, то диагонали этих кубов, проходящие через O, лежат на одной прямой. Поэтому из всех подобных кубов, которые можно поместить в параллелепипед, мы выберем максимальный.
Пусть с < а и с < b. Тогда в параллелепипед можно поместить куб с ребром с (рис. P.3.32).
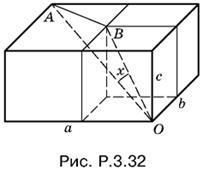
Вычислим все стороны треугольника ABO и воспользуемся теоремой косинусов:
AB² = AO² + BO² − 2AO · BO cos x,
AO² = а² + b² + с², BO² = 3c²,
AB² = (а − с)² + (b − с)².
Для определения cos x получим уравнение
![]()
которое симметрично относительно а, b и с, а потому не зависит от соотношения между этими величинами. Убедитесь сами в том, что cos x не будет больше единицы при любых а, b и с.
Ответ.
![]()
3.33. Разность углов А и С равна φ, BD — биссектриса угла B в треугольнике ABC (рис. P.3.33).
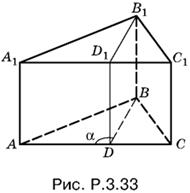
Вычислим угол а:
α = B/2 + С = π − A − C/2 + С = π/2 + C − A/2 = π/2 + φ/2.
Объем призмы равен произведению АА1 на площадь основания ABC, т. е.
АА1 (½AD · DB sin α + ½DC · DB sin α) = ½АА1 · DB · AC sin α = ½ aS cos φ/2.
Ответ. ½ aS cos φ/2.
3.34. Пусть выбраны диагонали С1D и В1С (рис. P.3.34). Так как В1С || А1D и С1D || В1A, то плоскости А1С1D и АВ1С параллельны. Расстояние между В1С и С1D равно расстоянию между этими плоскостями.
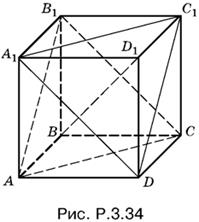
Обе плоскости А1С1D и АВ1С перпендикулярны к диагонали BD1. Поэтому искомое расстояние равно разности между отрезком BD1 и удвоенной высотой пирамиды D1А1С1D. Объем этой пирамиды равен a³/6, а площадь основания А1С1D равна а√3/2 , следовательно, высота h = a/√3. Так как BD1 = a√3, то искомое расстояние равно a√3 − 2a/√3 = a/√3.
Ответ. a/√3.
3.35. Из соображений симметрии ясно, что точка O лежит на диагонали AC1 куба. Для доказательства достаточно установить, что плоскость KMN (рис. P.3.35) перпендикулярна к АС1 и что АС1 проходит через точку O1, являющуюся центром треугольника KMN.
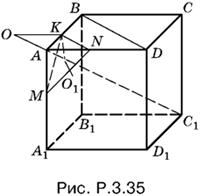
По теореме о трех перпендикулярах АС1 ⊥ BD. Следовательно, АС1 ⊥ KN. Аналогично прямая АС1 перпендикулярна к KM или MN, т. е. АС1 — перпендикуляр к плоскости KMN.
Треугольник KMN равносторонний. Так как AK = AN = AM, то из равенства соответствующих треугольников, имеющих общие вершины в точках А и О1, получаем KO1 = NO1 = MO1.
Мы доказали, что центр О сферы лежит на продолжении отрезка АС1.
Так как AK — биссектриса в треугольнике OKO1, то
![]()
. Отсюда найдем OK = R, выразив остальные отрезки через ребро куба:
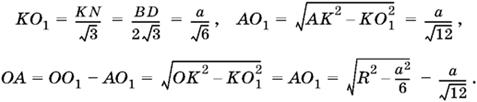
Подставив все эти выражения в пропорцию
![]()
, получим уравнение относительно R. После простых преобразований это уравнение запишется в виде
6R² − 2√6 aR − 3а² = 0.
Геометрический смысл имеет только положительный корень.
Ответ.
![]()
3.36. Докажем вначале, что каждая сторона четырехугольника параллельна биссектральной плоскости двугранного угла, образованного данными взаимно перпендикулярными плоскостями. Перенесем сторону четырехугольника параллельно себе так, чтобы одна из ее вершин лежала на ребре этого двугранного угла (рис. P.3.36, а). Полученный отрезок RS спроецируем на плоскости P и Q. Так как проекции при параллельном переносе не изменяются, то RS1 = RS2 = 1. Построим линейный угол S1TS1, измеряющий двугранный угол между плоскостями P и Q, и соединим точки S и T. Треугольники RS1T и RS2T и треугольники RS1S и RS2S попарно равны, т. е. прямоугольные треугольники S1ST и S2ST — равные и равнобедренные. Следовательно, углы STS1 и STS2 равны 45°, а это означает, что сторона данного четырехугольника параллельна биссектральной плоскости. Проведя аналогичные рассуждения для каждой стороны, придем к выводу, что плоскость четырехугольника параллельна биссектральной плоскости.
Перенесем теперь плоскость P параллельно так, чтобы четырехугольник уперся в нее одной из своих вершин, которую обозначим буквой А (рис. P.3.36, б).
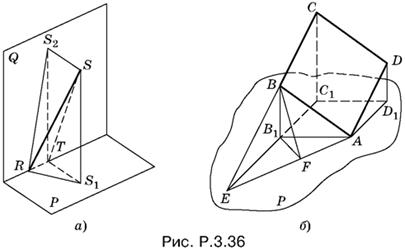
Спроецируем четырехугольник ABCD на плоскость P. Поскольку его проекция АВ1С1D1 — квадрат, то ABCD — параллелограмм. Поэтому один из отрезков AB или AD равен √5/2. Предположим, что это AB.
Построим теперь след, оставленный плоскостью четырехугольника ABCD на плоскости P. Для этого построим вначале точку E, в которой пересекаются прямые BC и В1С1, а затем соединим E и А. Угол между плоскостями ABCD и P измерим линейным углом BFB1, равным 45°. Остается провести вычисления:
![]()
следовательно, угол B1AF равен 30° и поэтому B1E = 1/√3; находим
![]()
и так как
![]()
, то BC = √7/2.
Ответ. √5 + √7 .
3.37. Опишем около данной пирамиды конус с образующей l, высотой H и радиусом нижнего основания R. Объем конуса больше объема пирамиды. Если мы докажем, что объем конуса меньше куба образующей, то задача тем самым будет решена.
Рассмотрим угол α между H и l. Тогда
H = l cos α, R = l sin α,
а объем конуса равен
V = π/3 R²H = π/3 l³ sin² α cos α.
Составим отношение:
V/l³ = ⅓π sin² α cos α = π/6 sin 2α sin α ≤ π/6 < 1,
что и доказывает сформулированное в условии утверждение.
3.38. B осевом сечении конуса получим картину, изображенную на рис. P.3.38.
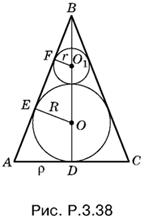
По условию r = pR. Из подобия треугольников ЕОВ и FO1B получим
r/R = H − 2R − r/H − R, т. е. H = 2R²/R − r,
а из подобия треугольников AOB и ОЕВ (AB = l) найдем
l/ρ = H − R/R, (5)
т. е.
l = ρH − R/R = ρ1 + p/1 − p.
Так как l² − ρ² = Н², получаем уравнение относительно ρ, решая которое находим ρ² = R²/p. Полная поверхность конуса равна πp(ρ + 1). С помощью производной пропорции из соотношения (5) получим
l + ρ/ρ = H/ρ, т. е. (l + ρ)ρ = ρ²H/R = 2R²/p(1 − p).
Сумма поверхностей шаров равна 4π(R² + r²).
Составим искомое отношение:
2(R² + r²)p(p − 1)/R² = 2(1 + p²)p(1 − p).
Ответ. 2p(1 − p)(1 + p²).
3.39. Обозначим радиус сферы через R и рассмотрим осевое сечение каждого из конусов. Второй конус можно расположить внутри сферы произвольным образом. Мы расположим его так, чтобы образующие обоих конусов были параллельны (рис. P.3.39). Выразим радиусы оснований конусов через R.
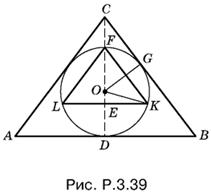
B треугольнике FOK углы OFK и OKF равны α/2· Следовательно, угол EOK равен их сумме, т. е. α. Из треугольника EOK находим EK = R sin α. Далее,
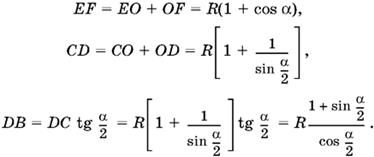
Составим теперь отношение объемов и приравняем его к a. После простых преобразований придем к уравнению относительно α:
![]()
Так как 1 + sin α/2 ≠ 0 (иначе не существует конус), то
![]()
откуда
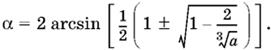
Чтобы можно было осуществить извлечение корня, необходимо взять а ≥ 8.
Так как а > 0, то выражение, стоящее под знаком арксинуса, как легко проверить, всегда расположено между 0 и 1.
Ответ.
![]()
3.40. Так как O1 — центр сферы, касающейся граней SAB и SAC в точках B и C (рис. P.3.40, а), то O1 лежит в плоскости, перпендикулярной к их общему ребру SA и проходящей через эти точки. При этом ED — биссектриса линейного угла ВЕС, измеряющего двугранный угол между рассматриваемыми плоскостями.
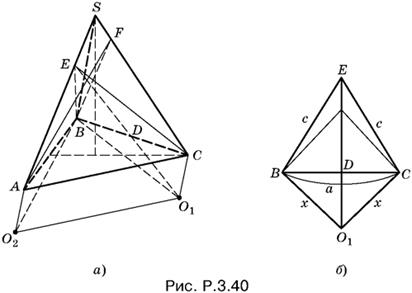
Если сделать такие же построения для второй сферы O2, то получим четырехугольник AFBO2, равный четырехугольнику BECO1 (равенство очевидно из соображений симметрии, однако этот факт легко устанавливается и непосредственно). Следовательно, CO1 = AO2 = BO2 = BO1. Заметим, что AO || CO1 как два перпендикуляра к плоскости ASC. Итак, O1O2 = AC = а.
Поскольку O1B ⊥ ASB, то O1B ⊥ SB, аналогично O2B ⊥ SB, откуда SB ⊥ O1BO2. Мы доказали, что SB — высота пирамиды SO1BO2.
Чтобы ответить на поставленный в задаче вопрос, остается вычислить длину отрезка BO1. Так как отрезок EC из треугольника ASC определяется легко:
EC² = a²/4b²(4b² − a²),
то дальнейшие вычисления нельзя проводить, оставаясь в плоскости BEC (рис. P.3.40, б). Обратим лишь внимание на тот факт, что треугольники BES и CES равны, т. е. BE = CE, откуда следует, что биссектриса ED является в треугольнике BEC и медианой. Фигура BECO1 — ромбоид (BC ⊥ EO1). Обозначим EC = с, BO1 = x. Треугольники ECO1 и ECD подобны. Поэтому ED : с = a/2 : x, откуда x = ac/2ED, т. е. x² = a²c²/4c² − a².
Подставляя вместо с = EC его выражение через а и b, получим
OB² = a²(4b² − a²)/4(3b² − a²).
Теперь можно определить высоту треугольника O1BO2, опущенную на O1O2. Она равна
![]()
Все элементы, необходимые для вычисления объема, сосчитаны.
Ответ.
![]()
3.41. Расстояние между центрами O1 и O3 двух не касающихся друг друга шаров равно 2r√2 (рис. P.3.41, а).
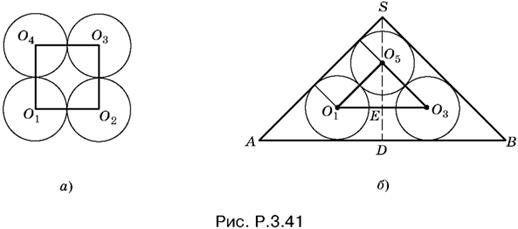
На рис. P.3.41, б изображено осевое сечение конуса, проходящее через O1 и O3. B этом же сечении будет лежать и O5. B треугольнике O5O1Е сторона O1O5 = 2r, а O1Е = r√2 , следовательно
![]()
т. е. угол O5O1Е равен 45°. Треугольник ASD подобен треугольнику O1O5Е . Поэтому H = R. Найдем H:
H = SO5 + O5E + ED = √2r + 2r/√2 + r = r(2√2 + 1).
Теперь можно найти и объем конуса:
V = πr³/3(2√2 + 1)³.
Ответ. πr³/3(22√2 + 25).
3.42. Так как ребро SD перпендикулярно к плоскости основания, то треугольник SCD (рис. P.3.42, а), в который вписана окружность основания цилиндра, прямоугольный.
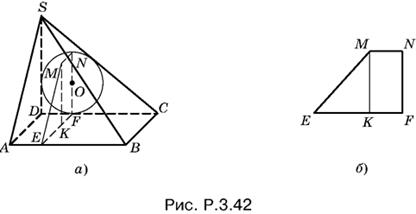
Радиус этой окружности равен частному от деления площади треугольника SDC на полупериметр, т. е.
![]()
Угол MEK равен углу SAD, так как треугольники MEK и SAD подобны. Из треугольника SAD находим ctg ∠ SAD = a/h. Следовательно, и ctg ∠ MEK = a/h. Для дальнейших рассуждений достаточно рассмотреть трапецию EMNF (рис. P.3.42, б).
Отрезок MK = 2r. Из треугольника MEK находим
EK = MK ctg ∠ MEK = 2ra/h.
Искомый отрезок
KF = EF − EK = a − 2ra/h = a(h − 2r)/h.
Ответ.
![]()
3.43. Пусть OA = R, SO = H, ребро куба равно a (рис. P.3.43).
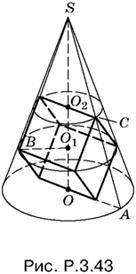
Из подобия треугольников SOA и SO1B получим
![]()
Так как
![]()
то
![]()
Из подобия треугольников SO1B и SO2C
![]()
Упростим последнюю пропорцию и найдем из нее H:
![]()
С помощью первого соотношения определим теперь R:
![]()
Остается сосчитать отношение объемов: πR²H/3a³.
Ответ.
![]()
3.44. Обозначим через а сторону нижнего основания пирамиды, через b сторону ее верхнего основания, а через S площадь боковой грани. Объем пирамиды можно записать так:
![]()
С другой стороны, объем равен
![]()
Приравнивая эти два выражения, найдем
![]()
Вспомним, что боковая грань — трапеция, боковые ребра которой равны верхнему основанию. Площадь этой трапеции легко найти, если вычислить ее высоту:
![]()
Сравнивая с предыдущим выражением для S, получим уравнение относительно а/b. После сокращения на а + b (равенство суммы а + b нулю не имеет геометрического смысла) и возведения в квадрат придем к выражению
2b² + ab − а² = 0
или
(a/b)² − a/b − 2 = 0.
Так как а и b — положительные величины, то а/b = 2, или а = 2b.
Чтобы связать величины b и r, спроецируем точку С1 на плоскость нижнего основания (рис. P.3.44). Поскольку радиус описанной окружности треугольника ABC в два раза больше радиуса описанной окружности треугольника А1В1С1, то DC = b/√3.
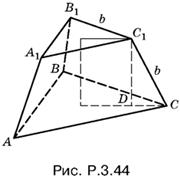
По теореме Пифагора для треугольника С1DС
b² − b²/3 = 4r²,
откуда
b = r√6, а = 2b = 2r√6.
Остается вычислить объем:
![]()
Ответ. 7√3r³.
3.45. Пусть О1 и О2 — центры меньших шаров, О3 — центр большого шара, а О — центр шара, радиус которого нужно определить. Спроецируем точки O1, O2, O3 и О на плоскость (рис. P.3.45). Треугольник Р1Р2Р3 равнобедренный и точка P лежит на его медиане и высоте.
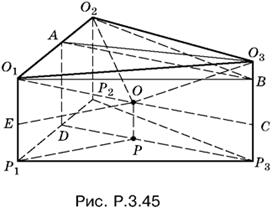
Обозначим радиус ОР = x. После этого многие отрезки на рис. P.3.45 можно будет выразить через R, r и x. Отложим на O3Р3 = R отрезок ВР3 = r. Треугольники O1O2В и Р1Р2Р3 равны, как основания призмы. Перед нами задачи — связать величины r = О1Р1 = О2Р2, R = О3Р3, x = ОР. Прямоугольные треугольники ОО1Е и ОО3С позволяют вычислить отрезки РР1 и Р3Р. Отрезок DР3 = AB можно найти из прямоугольного треугольника О3АВ (О3А можно считать известной величиной). Полученные отрезки образуют прямоугольный треугольник P1DP, для которого будут вычислены все стороны. Теорема Пифагора для этого треугольника и даст нужное нам соотношение между r, R и x.
Проведем теперь все вычисления.
Из треугольника О3АО2 находим
![]()
из треугольника О3АВ находим
![]()
Следовательно,
![]()
Вычисляем
P3Р² = CO² = (R + x)² − (R − x)² = 4Rx
и
Р1Р² = ЕО² = O1O² − O1Е² = (r + x)² − (r − x)² = 4rx.
B треугольнике P1DР известна гипотенуза Р1Р. Катет Р1D = r, а катет
![]()
По теореме Пифагора Р1Р² = Р1D² + DP², т. е.
![]()
или
![]()
Решая это уравнение, находим
![]()
Хотя правая часть в обоих случаях положительна, нужно взять только знак минус, так как второе значение для √x оказывается больше √r, что невозможно.
Ответ.
![]()
3.46. Пусть O1 и O2 — центры двух равных шаров с радиусом R, а O3— центр третьего шара радиусом r (рис. P.3.46). Треугольник O1O3F прямоугольный, т. е.
O1O3² = O1F² +O3F².
Так как O1O3 = R + r, O1F = R − r, то остается вычислить O3F. Из треугольника BDE, в котором DB = O3F, имеем
DB² = DE² + ЕВ².
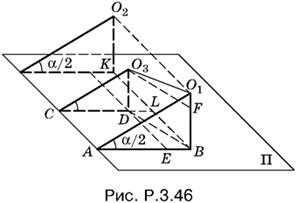
Длину отрезка EB можно найти как AB − AE. Но AB = R ctg α/2 (из треугольника O1AB), а AE = CD = r ctg α/2 (из треугольника O2CD). Таким образом,
EB² = (R ctg α/2 − r ctg α/2)².
Отрезок DE можно определить, если воспользоваться условием, что шары O1 и O2 касаются. Отрезок O1O2 равен 2R и параллелен плоскости Π. Следовательно, KB = 2R и DE = LB = R.
Величина DB² теперь найдена:
DB² = R² + ctg² α/2 (R − r)²,
и теорема Пифагора для треугольника O1O3F примет вид
(R + r)² = (R − r)² + R² + ctg² α/2 (R − r)².
Раскрыв скобки в членах, не содержащих множителя ctg² α/2, найдем
ctg² α/2 = 4Rr − R²/(R − r)².
По условию r/R = m; разделим числитель и знаменатель правой части почленно на R²

Число m всегда меньше единицы, так как по условию r меньше R. Кроме того, 4m − 1 ≥ 0, так как слева стоит квадрат. Но ctg α/2 = 0, если α/2 = π/5 и α = π, что невозможно. Поэтому 4m − 1 > 0 и m > ¼.
Ответ. При ¼ < m < 1
![]()
3.47. Обозначим центры шаров буквами O1, O2 и O3, а их проекции на плоскость P через A, B и C. Треугольник ABC (рис. P.3.47) равносторонний со стороной 2R, а точка O — проекция вершины S конуса — будет центром этого треугольника.
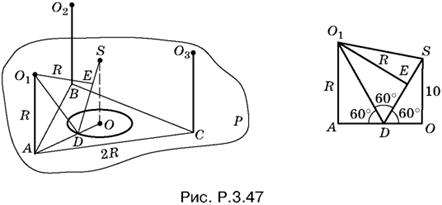
Образующую конуса, которой касается шар с центром в точке O1, обозначим через SD, а точку касания — буквой E. Отрезок O1E перпендикулярен SD и равен R. Так как данный конус равносторонний, то угол между образующей и ее проекцией на основание конуса равен 60°. По условию SO = 10, следовательно, DO = 10 · ctg 60° = 10/√3. Отрезок AO находим из треугольника ABC:
AO = 2R /√3.
Таким образом, AD = 2R − 10/√3. Угол ADE равен 120°, а луч O1D делит его пополам. Из прямоугольного треугольника AO1D
R = AD tg 60°, т.е. R = 2R − 10/√3 √3.
откуда находим R.
Ответ. 10 см.
3.48. Пусть SO1 и SO2 — оси соседних конусов (рис. P.3.48). Тогда середина C отрезка O1O2 лежит на общей образующей этих конусов.
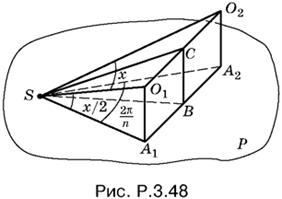
Угол O1SO2 равен углу в осевом сечении конуса, обозначим его через x. Тогда углы O1SA1 и О2SA2 равны x/2. Проекции осей SO1 и SO2 на плоскость P лежат на образующих, по которым происходит касание конусов с плоскостью P. Так как конусов n, то угол A1SA2 = 2π/n.
Отрезок SO1 можно выразить через А1В двумя способами:
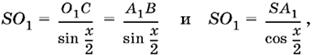
а так как
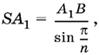
то
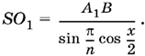
Приравнивая полученные для SO1 выражения, получим tg x/2 = sin π/n.
Ответ. x = 2 acrtg [sin π/n].
3.49. Так как угол AOB (рис. P.3.49, а, б) прямой, то точки А и О лежат на сфере, построенной на AB, как на диаметре. Следовательно, все внутренние точки отрезка АО лежат внутри этой сферы. Поскольку центр сферы, радиус которой мы ищем, лежит на АО, то возможно лишь внутреннее касание сфер.
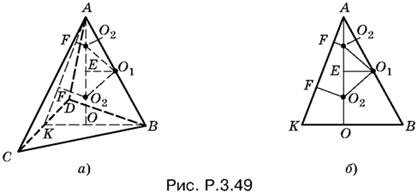
Центр О2 вписанной сферы соединим с точкой F, в которой происходит касание сферы с одной из граней. Из подобия треугольников FО2A и OKA имеем
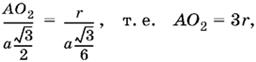
где r — искомый радиус.
Спроецируем точку О1 на АО и рассмотрим прямоугольный треугольник O1EO2. B нем O1O2 равно разности радиусов, т. е. O1O2 = a/2 − r; EO1 равно половине OB, т. е. EO1 = а√3/6. Отрезок O2Е = |AE − AO2|. Знак абсолютной величины означает, что точка О2 может оказаться ниже точки E, либо выше ее (см. рис. P.3.49, на котором изображены оба случая). Так как AE = ½, АО = a/√6, а AO2 = 3r, то O2E = |a/√6 − 3r|.
По теореме Пифагора O2O²1 = O2Е² + EO²1, т. е.
(a/2 − r)² = (a/√6 − 3r)² + a²/12.
После простых преобразований получим уравнение
8r² + (1 − √6)ar = 0,
откуда
r = √6 − 1/8а.
Так как АO2 = 3r, то AO2 = 3√6 − 1/8а, в то время как AE = a/√6.
Сравнивая AO2 и AE, мы видим, что AO2 больше. Следовательно, точка O2 на рис. P.3.49 должна располагаться ниже точки E.
Ответ. √6 − 1/8а.
3.50. Плоскость Π, проходящая через ось РР и центр О основания пирамиды, образует в сечении некоторый треугольник SMN (рис. P.3.50). Повернем треугольник SAB около оси РР так, чтобы он лег в плоскость Π. Так как AB = MN, а высота SO меньше высоты SK, то треугольники расположатся так, как показано на рис. P.3.50. Любое другое сечение SEF пирамиды попадет внутрь пятиугольника SMABN, а все сечения дважды покроют этот пятиугольник.
Остается определить объем тела, полученного от вращения пятиугольника SMABN вокруг оси РР. Половину искомого объема можно получить в виде разности объемов цилиндра, полученного от вращения прямоугольника SKBL, и конуса, полученного от вращения треугольника SNL:
½VSMABN = VSKBL − VSNL = πSK² · BK − ⅓πLN² · BK = πBK(SK² − ⅓LN²).
Из соответствующих треугольников находим
SK = a/2 ctg α/2; LN² = SO² = SN² − NO² = a²/4 ctg² α/2 − a²/4.
Таким образом,
VSMABN = πa(a²/4 ctg² α/2 − ⅓a²/4 ctg² α/2 + a²/12) = πa³/12(2 ctg² α/2 +1).
Ответ. πa³/12(2 ctg² α/2 +1).
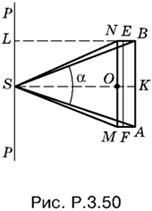
3.51. Способ 1. Рассмотрим радиус r вписанного в конус шара и угол α (на рис. P.3.51 изображено осевое сечение конуса).
Тогда полная поверхность конуса будет равна
Sпк = πR (R + l) = πr² ctg² α (1 + 1/cos 2α),
где радиус R основания конуса и его образующая l равны соответственно
R = r ctg α, l = r ctg α/cos 2α.
(промежуточные выкладки проделайте самостоятельно). Так как Sш = 4πr² и по условию Sпк = 2Sш, то после сокращения на πr² и несложных преобразований приходим к тригонометрическому уравнению
1 + cos 2α/cos 2α = 8 tg² α.
Выразив tg² α через cos 2α, получим
1 + cos 2α/cos 2α = 81 − cos 2α/cos 2α,
откуда cos 2α = ⅓.
Найдем теперь требуемое отношение объемов. Имеем
Vк = πr³/3 ctg³ α tg 2α, Vш = 4/3πr³.
Преобразуем выражение ctg³ α tg 2α, имея в виду, что cos 2α = ⅓:
ctg³ α tg 2α = ctg² α · ctg α sin 2α/cos 2α = 1 + cos 2α/1 − cos 2α · cos α · 2 sin α cos α/⅓ sin α = 8.
Следовательно, Vк = 2Vш, т. е. отношение объема конуса к объему шара равно 2.
Способ 2. Представим объем конуса как сумму двух объемов V1 и V2, где V1 — объем тела, образуемого вращением заштрихованного на рис. P.3.51 треугольника вокруг оси конуса, а V2 — объем конуса с осевым сечением AOB. Имеем
Vк = V1 + V2 = ⅓rSб + ⅓rSo = r/3(Sб + So) = r/3Sпк
(здесь использована лемма об объеме тела вращения треугольника; So — площадь основания конуса, Sб — площадь его боковой поверхности).
Так как Vш = r/3(4πr³) = r/3Sш, то
Vк : Vш = (r/3Sпк) : (r/3Sш) = 2.
Ответ. Отношение объемов равно 2.
3.52. Предположим, что двум равновеликим граням принадлежит ребро BB1. Спроецируем точку B1 на плоскость основания и обозначим проекцию буквой O. Если B1E и B1D — соответственно высоты параллелограммов CC1B1B и AA1B1B, то B1D = B1E, поскольку площади и основания у этих параллелограммов равны. Следовательно, прямоугольные треугольники B1OE и B1OD равны, т. е. точка O находится на одинаковом расстоянии от прямых AB и CB. Поэтому (подробнее см. задачу 5.4) она лежит на биссектрисе одного из углов, образованных этими прямыми. Случаю, когда точка O находится либо внутри угла ABC, либо попадает в угол, вертикальный по отношению к углу ABC, отвечает рис. P.3.52, а. Другой возможный вариант изображен на рис. P.3.52, б. Здесь в построении участвует биссектриса угла ABN.
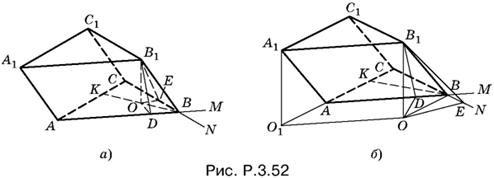
Начнем с первого случая. Так как ABC — правильный треугольник, то BK ⊥ AC и, следовательно, В1В ⊥ AC. Поскольку ребро A1A параллельно В1В, то А1A ⊥ AC. Мы доказали, что в первой из двух различных ситуаций АА1С1С — прямоугольник. Если AB = а, A1A = b, то S2 = ab. Чтобы связать введенные элементы с известными из условия задачи, вспомним, что треугольник, лежащий в основании, правильный. Следовательно, OB = 2 · OD (угол OBD равен π/6). Отрезок OD найдем из треугольника В1OD, а отрезок OB — из треугольника В1OB.
Итак,
![]()
благодаря чему
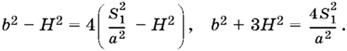
Поскольку
![]()
получаем возможность определить а:
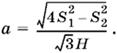
(6)
Рассмотрим теперь второй из возможных случаев (см. рис. P.3.52, б). Теперь ВО и AC параллельны и ВО ⊥ KB. Поэтому KB ⊥ ВВ1 и, следовательно, KB ⊥ АА1. Мы установили, что параллелограмм АА1С1С лежит во втором случае в плоскости, перпендикулярной к плоскости основания призмы. Следовательно, высота А1O1 призмы принадлежит плоскости АА1С1С, т. е. Ha = S2, откуда
![]()
Возможен еще один случай, который является как бы совпадением двух разобранных вариантов — точка О совпадает с вершиной B. Тогда призма прямая и при S1 = S2 из формулы (6) получим
![]()
Поскольку в первом случае S1 = аВ1D, S2 = аВ1В и В1D < В1В, то первому случаю соответствует требование S1 < S2. Условие положительности подкоренного выражения 4 S²1 − S²2 приводит ко второму ограничению S2 < 2S1.
Для второго случая получаем S1 = аВ1D, S2 = aH. Так как В1D > H, то S1 > S2. Случай S1 = S2 можно отнести к этому случаю.
Ответ.
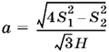
при S1 < S2 < 2S1, а = S2/H при S1 ≥ S2.
3.53. Проведем в кубе сечение AB1C1D (рис. P.3.53, а). Оно разобьет куб на две равные треугольные призмы. Возьмем одну из призм (рис P.3.53, б) и в качестве основания четырехугольной пирамиды выберем четырехугольник AB1C1D, а в качестве ее вершины точку D1. Оставшаяся часть призмы (D1AA1B1) образует треугольную пирамиду. Аналогично разобьем и вторую призму. Поскольку четыре пирамиды заполняют весь объем куба, их суммирующий объем максимален.
3.54. Пусть O1 — центр шара, описанного около пирамиды SABC, а O — центр правильного треугольника ABC, лежащего в ее основании. Тогда O1O — перпендикуляр к плоскости основания (рис. P.3.54).
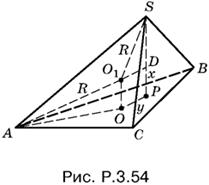
(По условию точка O1 равноудалена от A, B и C.) Обозначим длину отрезка O1O через x, а длину отрезка OP через y. Так как AO1 = SO1 = R, а AO = 6/√3 = 2√3, то по теореме Пифагора для треугольника AOO1 : x² + AO² = R², т. е. x² + 12 = R². Соотношение для y найдем из треугольника SO1D, где O1D = y, SO1 = R. Тогда SD² = R² − y². Но SD есть либо 4 − x, либо 4 + x в зависимости от расположения O1. Поэтому найдем x: x = |SP − SD|, что охватывает сразу два возможных случая и приводит к уравнению
![]()
Отсюда
![]()
Но x² = R² − 12, т. е.
![]()
Тогда
![]()
а после возведения в квадрат и приведения подобных членов: 64R² = 28² + 8у² + y4 или 64R² = (y² + 4)² + (28² − 16).
Поскольку
28² − 16/64 = 4² · 7² − 4²/4² · 4 = 7² − 1/4 = 48/4 = 12,
имеем R² = (y² + 4)²/64 + 12. Это выражение при x = 0 достигает своего минимального значения R² = 4²/64 + 12 = 12¼ = 49/4, т.е. R = 7/2.
Ответ. 3,5.
Замечание. Условие задачи, в силу которого основание P высоты SP пирамиды SABC принадлежит ее основанию ABC, при решении не использовано. Это условие оказалось лишним. Следовательно, в постановке задачи имеется неточность. Мы пытались использовать это условие, когда в первом указании строили прямую призму, верхнему основанию которой должна принадлежать вершина S. Эти ограничения оказались невостребованными при решении задачи. Задача реально предлагалась на вступительных экзаменах.