Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Задачи
Область определения. Периодичность
Областью определения функции может быть вся числовая ось (у = x², у = sin x), луч с принадлежащей ему граничной точкой (у = √x , граничная точка x = 0 принадлежит области определения x ≥ 0) и с не принадлежащей ему граничной точкой (у = lg x), совокупность интервалов (замкнутых, открытых, полуоткрытых) и отдельных точек.
Важной характеристикой функции является ее периодичность. С помощью периодических функций можно описать явления, повторяющиеся через равные промежутки времени. Функция f(x) называется периодической, если существует такое число T ≠ 0, что для любого значения аргумента x чи́сла x + T и x − T также являются значениями аргумента и выполняется равенство f(x + T) = f(x).
Если T — период f(x) и x — значение аргумента, то x + nТ, где n — целое число, — также значение ее аргумента, а пТ — период функции f(x). В частности, если T — период, то и −T — тоже период.
Наименьший положительный период называется основным периодом.
23.1. Найдите область определения функции
![]()
23.2. Найдите область определения функции
log3 log½ (x² − x − 1).
23.3. При каких значениях x выражение
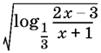
принимает действительные значения?
23.4. Найдите область определения функции
arccos (x² − 3х + 1) + tg 2х.
23.5. Где расположены точки плоскости, для координат которых выражение
![]()
принимает действительные значения ?
23.6. Докажите, что функция у = cos x² не является периодической.
23.7. Докажите, что если функция
f(x) = sin x + cos аx
периодическая, то а — рациональное число.
23.8. Найдите основной период функции
у = cos 3x/2 − sin x/3.