Функция y = ах2, ее график и свойства - Квадратичная функция и ее график - Квадратичная функция

Цель: рассмотреть свойства и график простейшей квадратичной функции у = ах2.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Разложите многочлен на множители.

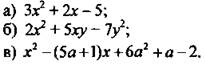
2. Сократите дробь.

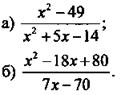
Вариант 2

1. Разложите многочлен на множители.

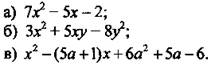
2. Сократите дробь.

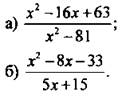
III. Изучение нового материала

Одной из наиболее распространенных и изученных функций является квадратичная функция у = ах2 + bх + с, где х - независимая переменная; а, b и с- некоторые числа (причем а ≠ 0).

Например, перемещение х тела при движении с ускорением а описывается квадратичной функций где x0 и V0 - положение и скорость тела в начальный момент времени t = 0.

С частным случаем квадратичной функции у = х2 (где а = 1, b = 0, с = 0) школьники уже знакомы. Графиком этой функции является парабола. Продолжим изучение квадратичных функций. Сначала ограничимся изучением функции у = ах2.

Пример 1

Составим таблицу значений и в одной системе координат построим графики функций

x	-2	-1,5	-1	-0,5	0	0,5	1	1,5	2
у = 1/2х2	2	1,12	0,5	0,12	0	0,12	0,5	1,12	2
у = х2	4	2,25	1	0,25	0	0,25	1	2,25	4
y = 2х2	8	4,5	2	0,5	0	0,5	2	4,5	8

Отметив на координатной плоскости точки, приведенные в таблице, построим графики данных функций. Видно, что при каждом значении х значения функции у = 1/2х2 в два раза меньше значений функции у = х2, а значения функции у = 2х2 в два раза больше значений функции у = х2. Другими словами, график функции у = 1/2х2 можно получить сжатием в два раза вдоль оси ординат графика функции у = х2. График функции у = 2х2 можно получить растяжением в два раза вдоль оси ординат графика функции у = х2.

Вообще говоря, график функции у = ах2 можно получить из параболы у = х2 растяжением вдоль оси ординат в а раз при а > 1 и сжатием вдоль оси ординат в 1/a раз при 0 < а < 1. График функции у = ах2 так же, как и график функции у = х2, называют параболой.

Приведем свойства функции у = ах2 при а > 0:

1. Область определения функции - промежуток (-∞; ∞).

2. Если х = 0, то у = 0. Следовательно, график проходит через начало координат.

3. Если х ≠ 0, то у > 0. Поэтому график расположен в верхней полуплоскости.

4. Функция четная, т. е. противоположным значениям аргумента соответствуют равные значения функции у(-х) = у(х). График функции симметричен относительно оси ординат.

5. Функция убывает в промежутке (-∞; 0] и возрастает в промежутке [0; ∞).

6. Функция ограничена снизу, у ≥ 0. Наименьшее значение у = 0 функция принимает при х = 0, наибольшего значения функция не имеет.

7. Область значений функции - промежуток [0; +∞).

Обсудим теперь свойства и график квадратичной функции у = ах2 при a < 0.

Пример 2

Составим таблицу значений и в одной системе координат построим графики функций у = 1/2х2 и у = -1/2х2.

x	-2	-1,5	-1	-0,5	0	0,5	1	1,5	2
у = 1/2х2	2	1,12	0,5	0,12	0	0,12	0,5	1,12	2
у = -1/2х2	-2	-1,12	-0,5	-0,12	0	-0,12	-0,5	-1,12	-2

Отметим точки, приведенные в таблице, и построим графики данных функций. Видно, что при каждом значении х значения функции у = -1/2х2 противоположны по знаку значениям функции у = 1/2х2. Поэтому график функции у = -1/2х2 получается из графика функции у = 1/2х2 с помощью симметрии относительно оси абсцисс.

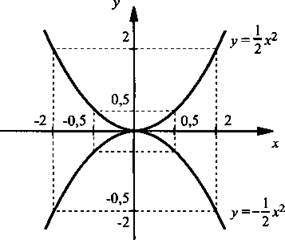
Теперь легко сформулировать свойства функции у = ах2 при а < 0:

1. Область определения функции - промежуток (-∞; ∞).

2. Если х = 0, то у = 0. Следовательно, график проходит через начало координат.

3. Если х ≠ 0, то у < 0. Поэтому график расположен в нижней полуплоскости.

4. Функция четная, у(-х) = y(x). График функции симметричен относительно оси ординат.

5. Функция возрастает в промежутке (-∞; 0] и убывает в промежутке [0; ∞).

6. Функция ограничена сверху, у ≤ 0. Наибольшее значение у = 0 функция принимает при х = 0, наименьшего значения функция не имеет.

7. Область значений функции - промежуток (-∞; 0].

Пример 3

Обсудим монотонность функции у(х) = ах2.

Область определения такой функции - все значения х. Рассмотрим два произвольных значения х2 и х1, такие, что х2 > x1. Найдем значения функции в этих точках: у(х2) = ах22 и у(х1) = ах12 и сравним их. Для этого определим знак разности у(х2) - у(х1) = ах22 – ах12 = а(х2 + х1)(х2 – х1).

Так как х2 > x1, то разность х2 – х1 положительна. Поэтому разность у(х2) - у(х1) определяется знаком произведения а(х2 + х1). Так как сумма х2 + х1 может иметь различный знак, то в области определения выделим два промежутка.

а) Для промежутка х ∈ [0; +∞) сумма х2 + х1 > 0. Поэтому знак разности у(х2) - y(х1) совпадает со знаком коэффициента а.

При а > 0 разность у(х2) - y(x1) > 0, т. е. у(х2) > у(х1) и функция возрастает.

При а < 0 разность у(х2) – y(х1) < 0 т. е. у(х2) < у(х1) и функция убывает.

б) Для промежутка х ∈ (-∞; 0] сумма х2 + x1 < 0. Поэтому знак разности у(х2) - y(х1) противоположен знаку коэффициента а.

При а > 0 разность у(х2) - y(х1) < 0, т. е. у(х2) < y(х1) и функция убывает.

При а > 0 разность у(х2) - y(х1) > 0, т. е. у(х2) > y(х1) и функция возрастает.

Пример 4

Построим график функции

Область определения функции задается условием 2х - 4 ≠ 0, т. е. х ≠ 2. Разложим числитель и знаменатель дроби на множители и сократим ее. Получаем:

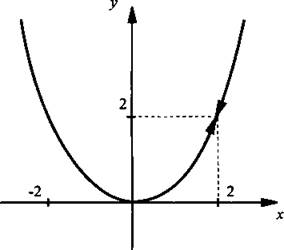
Построим параболу у = 1/2х2 и удалим из нее точку с абсциссой х = 2 (показана стрелками).

Пример 5

При каких значениях а парабола у = -1/2х2 и прямая у = 3х + а не имеют общих точек?

Предположим, что данные линии имеют общую точку. Тогда ее координаты удовлетворяют системе уравнений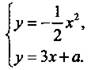

Попробуем решить эту систему. Так как в уравнениях левые части одинаковы, то равны и правые.

Получаем уравнение -1/2х2 = 3х + а, или 0 = х2 + 6х + 2а. На самом деле данные линии общих точек не имеют. Это означает, что полученное квадратное уравнение решений не имеет. Поэтому его дискриминант D = 36 - 8а < 0, откуда а > 36/8 = 4,5.

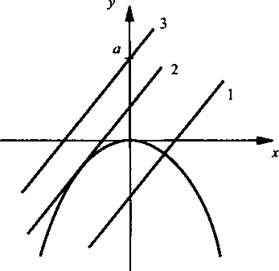
На рисунке приведена иллюстрация задачи. Очевидно, прямая у = 3х + а пересекает ось ординат в точке у = а. При увеличении а прямая смещается вверх параллельно самой себе. Выполненные расчеты показывают, что прямая при а < 4,5 пересекает параболу в двух точках (линия 1), при а = 4,5 касается параболы в одной точке (линия 2), при а > 4,5 не имеет общих точек с параболой (линия 3).

IV. Контрольные вопросы

1. Какая функция называется квадратичной?

2. Как называют график квадратичной функции?

3. Приведите основные свойства и график функции у = ах2 при а > 0.

4. Приведите основные свойства и график функции у = ах2 при а < 0.

5. Как из графика функции у = x2 получить график функции у = ах2 при а > 0.

V. Задание на уроке

№ 90; 92; 94; 96 (а, в); 97; 99; 101; 103 (а); 104 (а); 105.

VI. Задание на дом

№ 91; 93; 95; 96 (б, г); 98; 100; 102; 103 (б, в); 104 (б).

VII. Творческие задания

1. Постройте график функции.

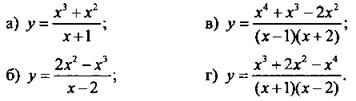
2. Постройте график уравнения или неравенства.

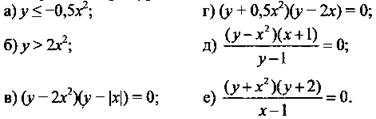
VIII. Подведение итогов урока