Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии - Геометрическая прогрессия - Арифметическая и геометрическая прогрессии
Цель: рассмотреть последовательность - геометрическую профессию.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Найдите сумму тридцати первых членов арифметической профессии, заданной формулой an = 3n + 2.
2. В арифметической профессии а6 = 1 и a10 = 13. Найдите сумму первых двадцати членов.
3. Найдите сумму всех трехзначных чисел, кратных 4.
Вариант 2
1. Найдите сумму сорока первых членов арифметической профессии, заданной формулой аn = 4n - 3.
2. В арифметической профессии a5 = 3 и а9 = 15. Найдите сумму первых тридцати членов.
3. Найдите сумму всех трехзначных чисел, кратных 3.
III. Изучение нового материала
Рассмотрим еще одну наиболее изученную последовательность - геометрическую профессию.
Последовательность чисел bn, первый член которой отличен от нуля и каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же отличное от нуля число q, называется геометрической прогрессией (q - знаменатель прогрессии): bn+1 = bnq (n ≥ 1, b1 ≠ 0, q ≠ 0).
Пример 1
Найти первые четыре члена геометрической профессии, если b1 = 2, q = 3.
Из определения геометрической прогрессии bn+1 = bnq имеем: при n = 1 b2 = b1q = 2 · 3 = 6, при n = 2 b3 = b2q = 6 · 3 = 18, при n = 3 b4 = b3q = 18 · 3 = 54. Итак, эти члены: 2, 6, 18, 54.
Геометрическая прогрессия задается рекуррентной формулой. При решении задач более удобна формула n-го члена.
Пример 2
Получим формулу n-го члена геометрической прогрессии.
Используем рекуррентную формулу bk+1 = bnq и выпишем (n - 1) равенство: 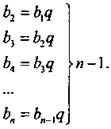 Перемножим почленно эти равенства. При этом в обеих частях равенства сократится произведение
Перемножим почленно эти равенства. При этом в обеих частях равенства сократится произведение ![]() Получаем
Получаем ![]() - формулу n-го члена геометрической прогрессии.
- формулу n-го члена геометрической прогрессии.
При решении задач, связанных с геометрической прогрессией, удобно выразить члены прогрессии через ее первый член и знаменатель.
Пример 3
Четвертый член геометрической прогрессии больше второго члена на 24, а сумма второго и третьего членов равна 6. Найти эту прогрессию.
Выразим второй, третий, четвертый члены прогрессии через ее первый член: ![]() и запишем условия задачи:
и запишем условия задачи: ![]()
Получим систему нелинейных уравнений 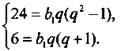
Разделив первое уравнение на второе, найдем: 4 = q - 1, откуда q = 5. Тогда из второго уравнения b1 = 1/5.
Пример 4
Первый член геометрической прогрессии b2, b2, b3, ... равен единице. При каком значении знаменателя прогрессии величина 4b2 + 5b3 имеет минимальное значение?
Выразив второй и третий члены прогрессии через ее первый член и знаменатель: b2 = b1q = q; b3 = b1q2 = q2, получим: S = 4b2 + 5b3 = 5q2 + 4q.
Квадратичная функция S(q) достигает минимального значения при ![]()
Пример 5
Пусть x1 и x2 - корни уравнения х2 – х + a = 0 и х3, х4 – корни уравнения х2 - 4х + b = 0. Известно, что числа х1, х2, x3, х4 (в указанном порядке) составляют возрастающую геометрическую прогрессию. Решить уравнения и найти числа а, b.
Для данных квадратных уравнений запишем формулы Виета: 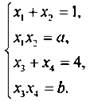
Рассмотрим сначала первое и третье уравнения этой системы и учтем, что ![]() Тогда получим:
Тогда получим: 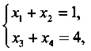 или
или 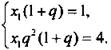 Разделив второе уравнение на первое, найдем q2 = 4, откуда q = 2 и q = -2 (не подходит, т. к. прогрессия возрастающая, т. e. q > 0).
Разделив второе уравнение на первое, найдем q2 = 4, откуда q = 2 и q = -2 (не подходит, т. к. прогрессия возрастающая, т. e. q > 0).
Из первого уравнения получаем: ![]() тогда х2 = 2/3, x3 = 4/3 и х4 = 8/3.
тогда х2 = 2/3, x3 = 4/3 и х4 = 8/3.
Из второго и четвертого уравнений исходной системы находим: ![]() Итак: х1 = 1/3, х2 = 2/3, х3 = 4/3, х4 = 8/3, а = 2/9, b = 32/9.
Итак: х1 = 1/3, х2 = 2/3, х3 = 4/3, х4 = 8/3, а = 2/9, b = 32/9.
Отметим еще одно важное свойство членов геометрической прогрессии. Квадрат любого члена прогрессии (начиная со второго) равен произведению соседних членов: ![]()
Пример 6
Докажем характеристическое свойство членов геометрической прогрессии.
Используя определение геометрической прогрессии, запишем: ![]()
При решении задач часто используется характеристическое свойство геометрической прогрессии.
Пример 7
При каких значениях х числа (х - 2); х; (х + 3) образуют геометрическую прогрессию?
Для решения этой задачи воспользуемся свойством геометрической прогрессии: квадрат члена прогрессии равен произведению членов с ним соседних. Так как ничего не сказано о порядке следования чисел, то в качестве среднего числа необходимо рассмотреть каждое из данных чисел.
а) Пусть (х - 2) - среднее по порядку число. Запишем свойство прогрессии: (х - 2)2 = х(х + 3), откуда х = 4/7, и имеем прогрессии: 4/7; -10/7; 25/7 (знаменатель равен -5/2) или 5/7; -10/7; 4/7 (знаменатель равен -2/5).
б) Пусть х - среднее из чисел. Тогда х2 = (х - 2)(х + 3), откуда х = 6.
Получаем прогрессии: 4; 6; 9 (знаменатель 3/2) или 9; 6; 4 (знаменатель 2/3).
в) Пусть (х + 3) - среднее из чисел. Тогда (х + 3)2 = х(х - 2), откуда х = -9/8. Находим прогрессии: -9/8; 15/8; -25/8 (знаменатель -5/3) или -25/8; 15/8; -9/8 (знаменатель -3/5).
Итак, при х = -9/8; х = 4/7; х = 6 данные числа образуют геометрическую прогрессию.
IV. Контрольные вопросы
1. Определение геометрической прогрессии.
2. Формула n-го члена геометрической прогрессии.
3. Характеристическое свойство геометрической прогрессии.
V. Задание на уроке
№ 623 (а, г); 624 (а, д); 625 (б, в); 627 (а, б); 630 (а); 631 (б); 633 (а); 634; 637; 639; 641; 643.
VI. Задание на дом
№ 623 (б, в); 624 (б, е); 625 (а, г); 627 (в, г); 630 (б); 631 (а); 633 (б, в); 635; 638; 640; 642; 644.
VII. Подведение итогов урока