Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Зачетная работа по теме «Уравнения и неравенства с одной переменной» - Неравенства с одной переменной - Уравнения и неравенства с одной переменной
Цепь: проверка знаний учащихся по вариантам одинаковой сложности.
Ход урока
I. Сообщение темы и цели урока
II. Варианты зачетной работ.
Вариант 1
А
1. Решите уравнение.
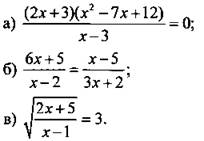
2. Решите неравенство.
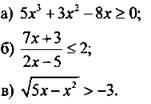
3. Найдите область определения функции ![]()
В
4. Решите уравнение.
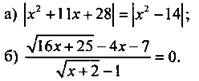
5. Решите неравенство ![]()
6. При каких значениях параметра а один корень уравнения х2 - 6х + 2а - 3 = 0 больше 2, а другой - меньше (-1)?
С
7. Решите уравнение (х2 + 4х + 3)2 + (х2 - 2х - 15)2 = 36(х + 3)2.
8. Решите неравенство (х2 - 2х + 9)(у2 + 4у + 7) ≤ 24.
9. Найдите все пары (х; у) целых чисел х и у, для которых выполнено неравенство ![]()
Вариант .
А
1. Решите уравнение.

2. Решите неравенство.

3. Найдите область определения функции ![]()
В
4. Решите уравнение.
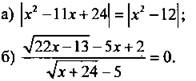
5. Решите неравенство ![]()
6. При каких значениях параметра а один корень уравнения х2 - 4х + 3a + 7 = 0 больше 1, а другой - меньше (-2)?
С
7. Решите уравнение (х2 + х - 20)2 + (х2 + 8х + 15)2 = 25(х + 5)2.
8. Решите неравенство (х2 - 4х + 7)(у2 + 2у + 10) ≤ 27.
9. Найдите все пары (х; у) целых чисел х и у, для которых выполнено неравенство ![]()
III. Ответы и решени.
Вариант 1
1. Ответ: а) -1,5; 4; б) 0; -2; в) 2.
2. Ответ: ![]()
3. Ответ: [-3; -2)U(-2; 1].
4. Ответ: а) -2; -7/2; -42/11; б) -1,5.
5. Ответ: 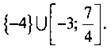
6. Ответ: (-∞; -2).
7. Для решения уравнения (х2 + 4х + 3)2 + (х2 - 2х - 15)2 = 36(х + 3)2 разложим квадратные трехчлены на множители и запишем уравнение в виде (х + 1)2(х + 3)2 + (х - 5)2(х + 3)2 = 36(х + 3)2. Очевидно, что корень такого уравнения х = -3. Найдем остальные корни. Поделим все члены уравнения на (х + 3)2 и получим квадратное уравнение (х + 1)2 + (х - 5)2 = 36, или х2 - 4х - 5 = 0. Его корни: х = -1 и х = 5.
Ответ: -3; -1; 5.
8. В данном неравенстве оценим каждый множитель: х2 - 2х + 9 = (х - 1)2 + 8 ≥ 8 (равенство достигается при х = 1) и y2 + 4y + 7 = (у + 2)2 + 3 ≥ 3 (равенство достигается при у = -2). Поэтому произведение (х2 - 2х + 9)(у2 + 4у + 7) ≥ 24. Следовательно, неравенство (x2 - 2х + 9)(у2 + 4у + 7) ≤ 24 выполняется только при х = 1 и у = -2. При этом неравенство становится равенством.
Ответ: х = 1, у = -2.
9. Для целых чисел х и у рассмотрим слагаемые в неравенстве ![]() Для таких х и у справедливы оценки:
Для таких х и у справедливы оценки: ![]() (равенство достигается при х = -4 и х = -6) и
(равенство достигается при х = -4 и х = -6) и ![]() (равенство достигается при у = 4 и у = 2). Сложив эти неравенства одного знака, получим:
(равенство достигается при у = 4 и у = 2). Сложив эти неравенства одного знака, получим: ![]() Поэтому данное неравенство выполняется только при х = -4 и у = 4, х = -4 и у = 2, х = -6 и у = 4, х = -6 и у = 2.
Поэтому данное неравенство выполняется только при х = -4 и у = 4, х = -4 и у = 2, х = -6 и у = 4, х = -6 и у = 2.
Ответ: х = -4, у = 4; х = -4, у = 2; х = -6, у = 4; х = -6, у = 2.
Вариант 2
1. Ответ: а) -2/3; -2; б) 0; -2; в) -6.
2. Ответ: 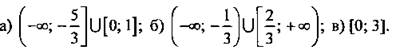
3. Ответ: [-5; -1)U(-1; 1].
4. Ответ: а) 4; 3/2; 36/11; б) 17/25.
5. Ответ: {-7}U[-4; -2,5].
6. Ответ: (-∞; -5/3).
7. Для решения уравнения (х2 + х - 20)2 + (х2 + 8х + 15)2 = 25(х + 5)2 разложим квадратные трехчлены на множители и запишем уравнение в виде (х - 4)2(х + 5)2+(х + 3)2(х + 5)2 = 25(х + 5)2. Очевидно, что корень такого уравнения х = -5. Найдем остальные корни. Поделим все члены уравнения на (х + 5)2 и получим квадратное уравнение (х - 4)2 + (х + 3)2 = 25, или х2 - х = 0. Его корни: х = 0 и х = 1.
Ответ: -5; 0; 1.
8. В данном неравенстве оценим каждый множитель: х2 - 4х + 7 = (х - 2)2 + 3 ≥ 3 (равенство достигается при х = 2) у2 + 2у + 10 = (у + 1)2 + 9 ≥ 9 (равенство достигается при у = -1). Поэтому произведение (х2 - 4х + 7)(у2 + 2у + 10) ≥ 27. Следовательно, неравенство (х2 - 4х + 7)(у2 + 2у + 10) ≤ 27 выполняется только при х = 2 и у = -1. При этом неравенство становится равенством.
Ответ: х = 2, у = -1.
9. Для целых чисел х и у рассмотрим слагаемые в неравенстве ![]() Для таких х и у справедливы оценки:
Для таких х и у справедливы оценки: ![]() (равенство достигается при х = -3 и х = -1) и
(равенство достигается при х = -3 и х = -1) и ![]() (равенство достигается при у = 3 и y = 5). Сложив эти неравенства одного знака, получим:
(равенство достигается при у = 3 и y = 5). Сложив эти неравенства одного знака, получим: ![]() Поэтому данное неравенство выполняется только при х = -3 и у = 3, х = -3 и у = 5, х = -1 и у = 3, х = -1 и у = 5.
Поэтому данное неравенство выполняется только при х = -3 и у = 3, х = -3 и у = 5, х = -1 и у = 3, х = -1 и у = 5.
Ответ: х = -3, у = 3; х = -3, у = 5; х = -1, у = 3; х = -1, y = 5.