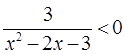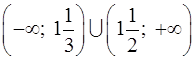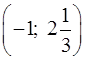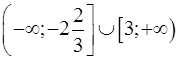Поурочные разработки по Алгебре 8 класс
Урок 3 - РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ
Цели: закрепить умение решать квадратные неравенства; рассмотреть решение различных заданий, с использованием квадратных неравенств; проверить умение учеников решать неравенства.
Ход урока
I. Организационный момент.
II. Индивидуальная работа.
Вызывается четыре ученика для самостоятельного выполнения заданий с карточек.
Карточка 1 Решите неравенство: x2 – 100 ≤ 0 |
Карточка 2 Решите неравенство:
|
Карточка 3 Найдите наибольшее целочисленное решение неравенства: –7x2 – 12x – 5 > 0 |
Карточка 4 Найдите наименьшее целочисленное решение неравенства: x2 + 3x + 2 ≥ 0 |
III. Актуализация знаний.
В момент выполнения индивидуальной работы остальные ученики самостоятельно выполняют задания № 34.28.
IV. Решение задач.
1) Рассмотреть решение различных заданий, с использованием неравенств № 34.23; 34.24; 34.33; 34.34; 34.36; 34.39; 34.44.
Сильным ученикам предлагается решить задачу № 34.46.
2) При каком наименьшем целом значении k уравнение 4y2 – 3y + k = 0 не имеет действительных корней?
3) Найдите область определения функций:
а) 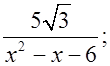 б)
б) 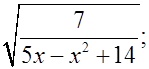 в)
в) 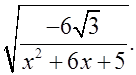
V. Самостоятельная работа.
Вариант 1 |
Вариант 2 |
1) Решить неравенства: |
|
а) 17x – 6x2 < 12; б) 0,5x2 – 12 ≤ 0; в) 4x2 + 1 ≤ –4x; г) 3x2 – 4x < 7. |
а) 20 < –4x2; б) 20x – 25x2 < 4; в) x – 3x2 ≥ –24; г) –3x2 ≥ 4x. |
2) При каких значениях параметра a квадратное уравнение x2 + ax + a – 1 = 0 имеет два различных корня? |
2) При каких значениях параметра a квадратное уравнение x2 – ax – a – 1 = 0 не имеет корней? |
О т в е т ы:
В а р и а н т 1
1 (а) |
1 (б) |
1 (в) |
1 (г) |
|
|
–0,5 |
|
2) Чтобы уравнение x2 + ax + a – 1 = 0 имело два корня, необходимо условие |
|||
В а р и а н т 2
1 (а) |
1 (б) |
1 (в) |
1 (г) |
|
|
|
|
2) Не существует таких значений параметра a, при которых уравнение x2 – ax – a – 1 = 0 не имело бы корней. |
|||
VI. Подведение итогов.
Домашнее задание: решить задачи № 34.26; 34.37; 34.40; 34.45.