Поурочные разработки по Алгебре 8 класс
Урок 1 - ФОРМУЛЫ КОРНЕЙ КВАДРАТНЫХ УРАВНЕНИЙ
Цели: показать способ решения полных квадратных уравнений с использованием формулы корней квадратного уравнения; формировать умение решать квадратные уравнения.
Ход урока
I. Организационный момент.
II. Анализ самостоятельно работы.
Выставить оценки за самостоятельную работу. Учащимся, не справившимся с данной работой, домой даются задания:
1) Привести уравнения к стандартному виду и выписать их коэффициенты:
а) 3x + 5x2 – 1 = 0;
б) 5x – 2 + x2 = 0;
в) x2 – 2 = 0.
2) Являются числа 3, 1, 0, –4 корнями уравнения x2 + 3x – 4 = 0.
3) Решить уравнения:
а) x2 – 3x = 0;
б) x2 – 16 = 0;
в) x2 – 2x + 1 = 0;
г) x2 + 4 = 0.
III. Актуализация знаний.
Рассмотреть решение уравнений:
а) 3x2 – 75 = 0;
б) x2 – 14x + 49 = 0;
в) x2 – x – 2 = 0.
IV. Объяснение нового материала.
Провести беседу с учениками и обсудить: всегда ли удобно решать уравнения графическим способом, сделать соответствующие выводы.
После этого учитель показывает способ решения квадратного уравнения с помощью формулы корней квадратного уравнения. Объяснение данной темы проходит согласно параграфу. Все формулы выписываются на доску. Для того, чтобы учащиеся лучше усвоили данную тему, можно приготовить плакат:

Для закрепления данного материала рассмотреть решение квадратного уравнения x2 – x – 2 = 0 через дискриминант, обсудить удобство данного решения.
x2 – x – 2 = 0;
a = 1, b = –1, c = –2;
D = b2 – 4ac = 12 – 4![]() 1
1![]() (–2) = 1 + 8 = 9 = 32;
(–2) = 1 + 8 = 9 = 32;
D = 9 > 0, значит имеем два действительных корня.
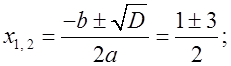
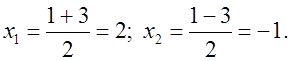
О т в е т: 2, –1.
V. Закрепление нового материала.
1) Рассмотреть решение уравнений № 25.4; 25.6; 25.8; 25.16; 25.18.
2) Сильным учащимся можно предложить следующие задания:
а) Найдите 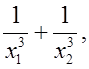 где x1 и x2 корни уравнения x2 – 3x – 6 = 0.
где x1 и x2 корни уравнения x2 – 3x – 6 = 0.
Р е ш е н и е:
x2 – 3x – 6 = 0;
a = 1, b = –3, c = –6;
D = b2 – 4ac = 9 – 4![]() 1
1![]() (–6) = 9 + 24 = 33;
(–6) = 9 + 24 = 33;
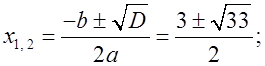
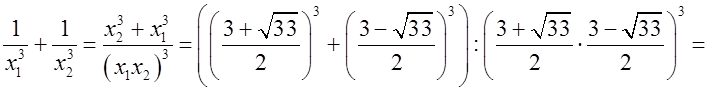
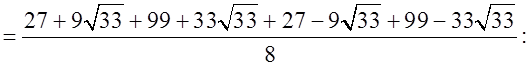
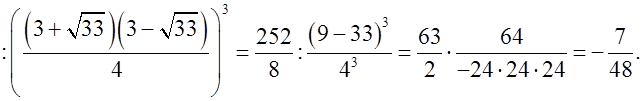
б) Один из корней уравнения 2x2 – 3x – 2 = 0 является так же корнем уравнения 2x2 – 5x + 2 = 0. На сколько этот корень меньше 5? (решения уравнений можно рассмотреть по вариантам).
в) При каком значении a уравнение 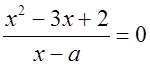 имеет один корень?
имеет один корень?
Р е ш е н и е:
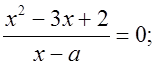
Чтобы дробь равнялась нулю, надо чтобы числитель дроби был равен нулю, а знаменатель – отличен от нуля. Решим уравнение:
x2 – 3x + 2 = 0;
a = 1, b = –3, c = 2;
D = b2 – 4ac = 9 – 8 = 1;
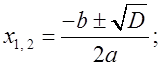
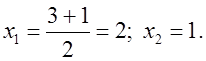
Уравнение 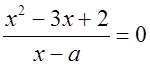 имеет два корня при условии а ≠ 1; а ≠ 2. По условию требуется найти для данного уравнения только один корень. Чтобы остался только один корень уравнения, необходимо, чтобы один из корней не входил в область допустимых значений. Значит a = 2 или a = 1, так как на ноль делить нельзя.
имеет два корня при условии а ≠ 1; а ≠ 2. По условию требуется найти для данного уравнения только один корень. Чтобы остался только один корень уравнения, необходимо, чтобы один из корней не входил в область допустимых значений. Значит a = 2 или a = 1, так как на ноль делить нельзя.
О т в е т: a1 = 2, a2 = 1.
VI. Подведение итогов.
Домашнее задание: прочитать материал параграфа 25 и выучить правила на с. 138–147. Решить уравнения № 25.2; 25.5.