ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ - урок 3

Цели: закрепить умение построения графиков различных функций, умение решать уравнения и системы уравнений графическим способом.

Ход урока

I. Организационный момент.

II. Актуализация знаний.

1) Проверить устно домашнее задание. Разобрать задания, которые вызвали у учащихся затруднения.

2) Назовите координаты вершин параболы:

а) y = 2x2; б) y = –3(x – 1) 2; в) y = 2(x + 3) 2 – 5;

г) y = x2 – 2x + 7; д) y = x2 + 3; е) y = –x2 + 2x + 3.

3) Какое из данных чисел – 2, 1, 3, 0, – 1 является корнем для уравнения:

а) x2 – 2x = 0; б) x2 – 4x + 3 = 0; в)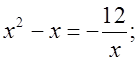

г) 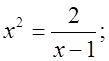д) x2 – 1 = 0; е) x2 + 4x – 5 = 0.

III. Решение задач.

Повторить правила решения и оформления следующих заданий по данной теме:

1) Постройте график данной функции и запишите ее свойства (по вариантам):

а) y = 2x2 – 3; б)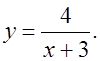

Так же ответить по получившимся рисункам на вопросы:

1. Возрастает или убывает функция на промежутке (–2; 1);

2. Найдите минимальное значение функции на интервале [1; +∞);

3. Найдите максимальное значение функции на отрезке [–2; 0].

(Учащимся, быстро справившимся с данным заданием, предлагается решить задание № 19.57.)

2) Повторить правила решения уравнений и систем уравнений графическим способом, рассмотрев задания № 17.27 (а, г); 17.33 (а, г); 18.17 (а, г); 19.47 (а, г); 22.23; 23.22.

3) Рассмотреть построение графиков различных функций на примерах № 17.44; 18.36; 21.29.

IV. Тестирование.

Подготовку к контрольной работе можно провести и как самостоятельное тестирование по вариантам.

В а р и а н т 1

1) В каких четвертях располагается график функции y = –2x2?

а) I и II; б) II и III; в) III и IV; г) I и IV.

2) Как изменяется график функции ?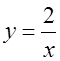

а) возрастает; б) убывает;

в) возрастает на промежутке (–∞; 0), убывает на промежутке (0; +∞);

г) убывает на промежутке (–∞; 0), возрастает на промежутке (0; +∞).

3) Найдите ординату точки, ограничивающей функцию y = 3x2 – 4 снизу.

а) 3; б) 4; в) – 4;

г) данная функция снизу не ограничена.

4) Найдите координаты вершины параболы, заданной функцией y = –4(x – 1) 2 – 3.

а) (–1; –3); б) (1; 3); в) (–1; 3); г) (1; –3).

5) Ветви какой параболы направлены вверх?

а) y = x2 – 2x – 5; б) y = 2x – x2 – 5;

в) y = 5 – 2x – x2; г) y = –x2 + 2x + 5.

6) Найдите наименьшее значение функции 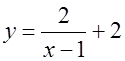на интервале (–∞; 0].

а) не существует; б) – 1; в) 0; г) 1.

7) Найдите координаты вершины параболы, заданной функцией y = –2x2 – 16x + 1.

а) (4; – 95); б) (– 4; 33); в) (8; – 255) г) (– 8; 1).

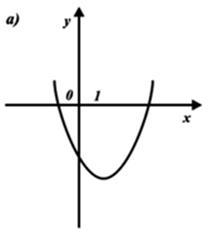
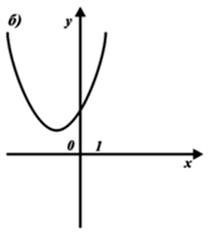
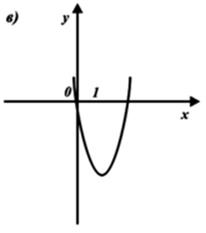
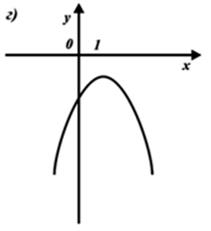
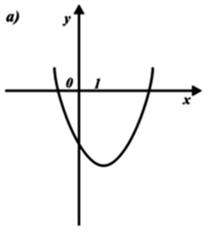
8) Выберите график функции y = x2 – 2x – 2.

В а р и а н т 2

1) В каких четвертях располагается график функции ?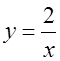

а) I и II; б) I и III; в) II и IV; г) I и IV.

2) Как изменяется график функции y = –3x2?

а) возрастает; б) убывает;

в) возрастает на промежутке (–∞; 0), убывает на промежутке (0; +∞);

г) убывает на промежутке (–∞; 0), возрастает на промежутке (0; +∞).

3) Найдите ординату точки, ограничивающей функцию y = 4 + 3x2 сверху.

а) 3; б) 4; в) – 4;

г) данная функция сверху не ограничена.

4) Найдите координаты вершины параболы, заданной функцией y = 2(x + 5) 2 – 1.

а) (–5; –1); б) (5; –1); в) (–1; 5); г) (1; –5).

5) Ветви какой из заданных парабол направлены вниз?

а) y = x2 + 2x – 5; б) y = 2x + x2 – 5;

в) y = 5 + 2x – x2; г) y = –5 + x2 – 2x.

6) Найдите наибольшее значение функции y = 0,5(x + 1)2 + 1 на интервале [–1; +∞).

а) не существует; б) – 1; в) 0; г) 1.

7) Найдите координаты вершины параболы, заданной функцией y = 3x2 + 18x + 25.

а) (3; 106); б) (– 3; – 2); в) (– 3; – 56) г) (3; 49).

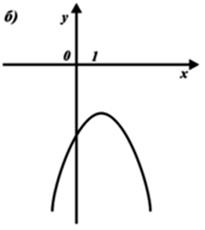
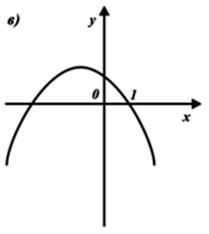
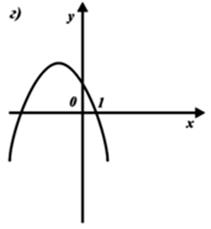
8) Выберите график функции y = –x2 – 2x + 1.

О т в е т ы:

	1	2	3	4	5	6	7	8
I	В	Б	В	Г	А	В	Б	А
II	Б	В	Г	А	В	А	Б	Г

Ответы проверяются на уроке, выборочно выставляются оценки. Те задания, которые вызвали затруднения, разбираются на доске.

V. Подведение итогов.

Домашнее задание: решить задания № 19.47 (б, в); 17.45; 21.25; 23.23.